Which Of The Following Is A Measure Of Variability

In an era increasingly driven by data, understanding how information is spread out is paramount. From scientific research to financial analysis, pinpointing the right tool to gauge variability is crucial.
The question of "Which of the following is a measure of variability?" often arises in statistics and data analysis contexts, highlighting a need for clarity and precision in choosing the correct analytical approach. This article explores the common measures of variability and their appropriate uses, informing data consumers and analysts alike.
Understanding Variability
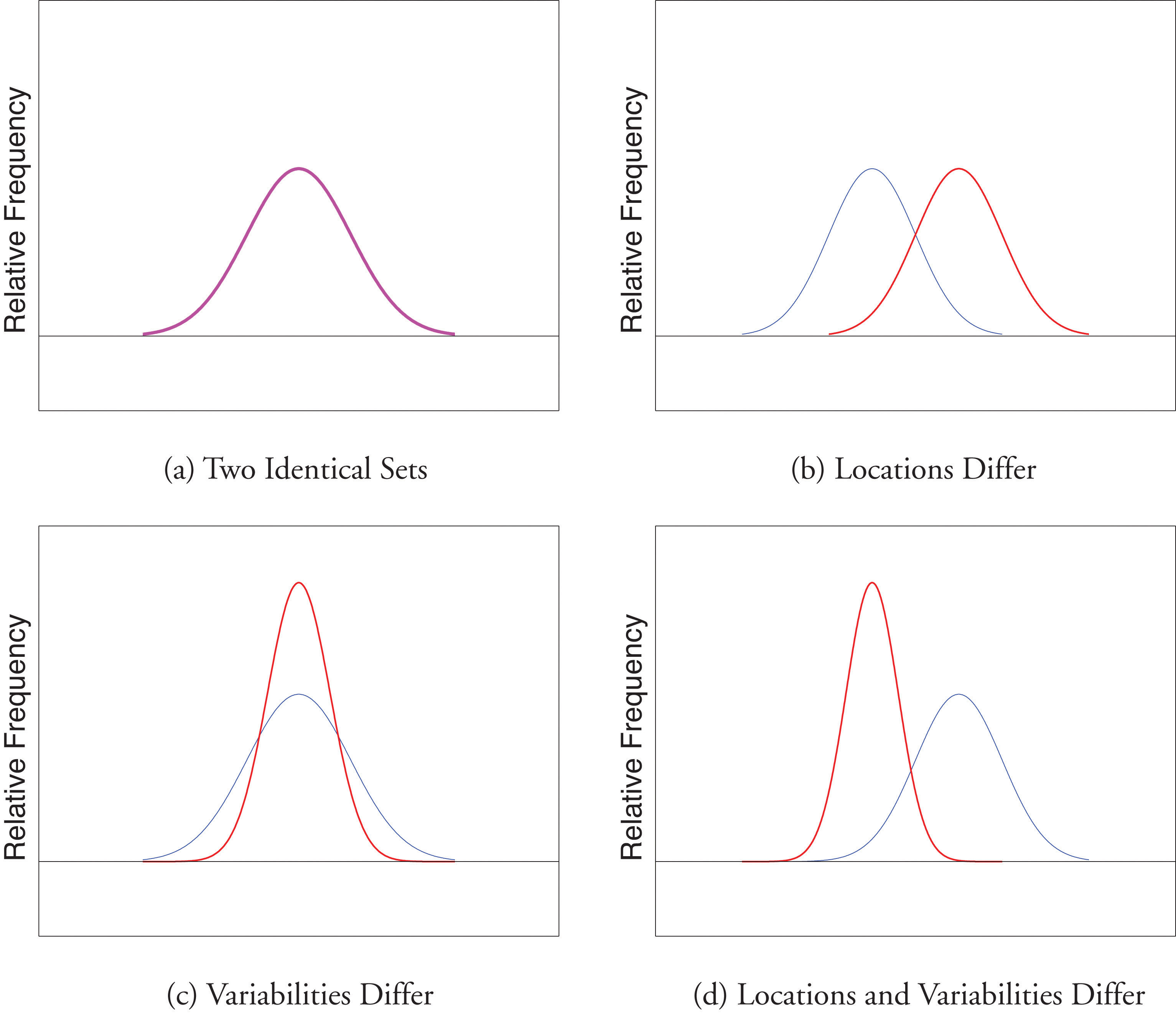
Variability, also known as dispersion, refers to the extent to which data points in a statistical distribution differ from each other, from the mean, or from some other central value. Different measures quantify this spread, each with its own strengths and weaknesses.
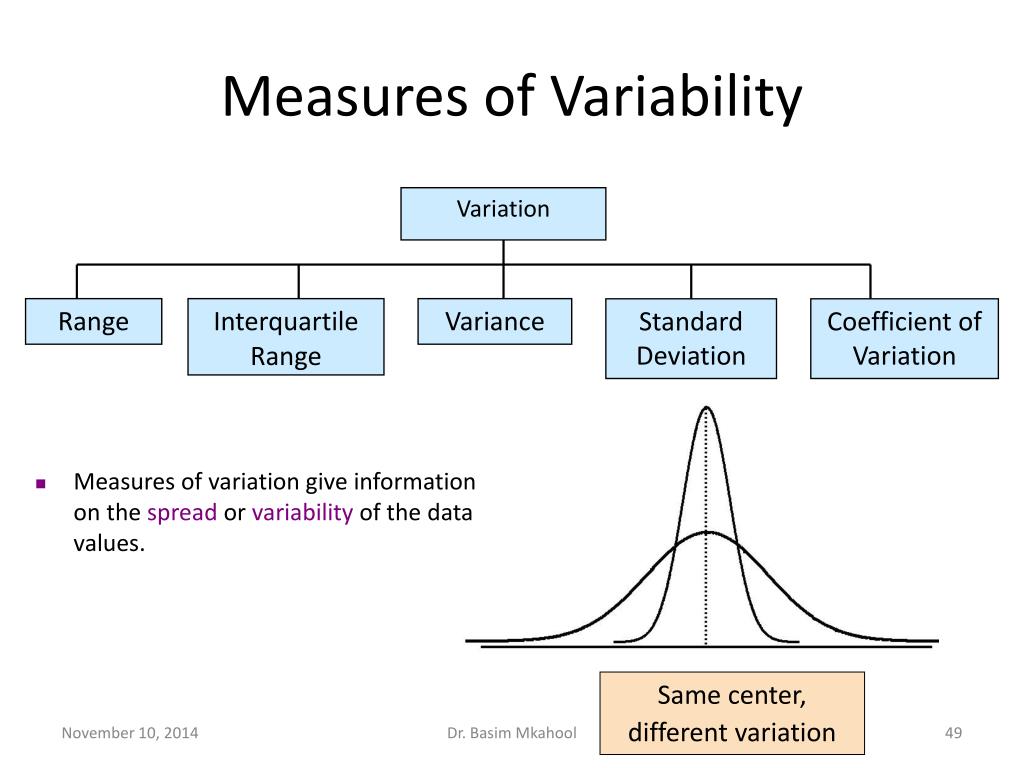
Range
The range is the simplest measure of variability, calculated as the difference between the largest and smallest values in a dataset. It’s easy to compute but highly sensitive to outliers, offering limited insight into the distribution between the extremes.
"The range is a quick, albeit crude, indicator of how spread out the data is," said Dr. Anya Sharma, a statistical consultant at Data Insights Group.
Interquartile Range (IQR)
The IQR is the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of a dataset. This measure focuses on the middle 50% of the data, making it more resistant to outliers than the range.
It's commonly used in box plots to visually represent the spread and identify potential outliers.
Variance
Variance measures the average squared deviation of each data point from the mean. A higher variance indicates greater dispersion, meaning data points are, on average, further from the mean.
While mathematically important, variance is expressed in squared units, making it difficult to interpret in the original data context. Variance serves as a building block for calculating the standard deviation.
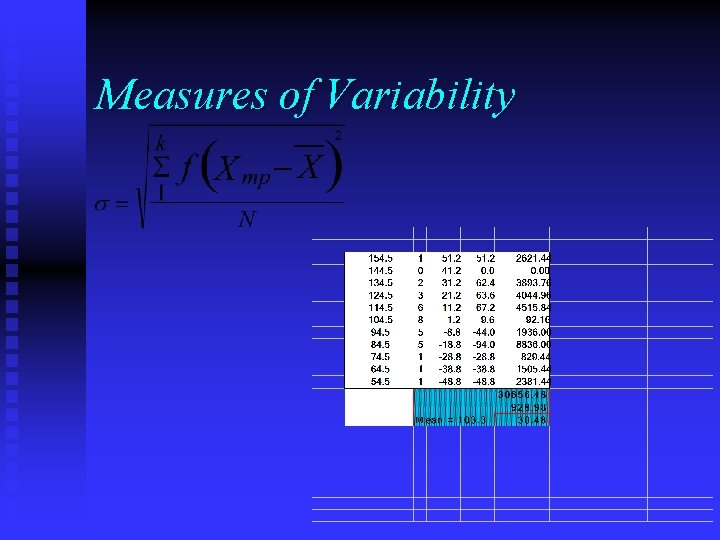
Standard Deviation
Standard deviation is the square root of the variance and represents the average distance of data points from the mean. It is expressed in the same units as the original data, making it more intuitive and widely used than the variance.
A lower standard deviation indicates that data points are clustered closer to the mean, while a higher standard deviation suggests greater spread.
Coefficient of Variation (CV)
The coefficient of variation (CV) is a standardized measure of dispersion that expresses the standard deviation as a percentage of the mean. This makes it useful for comparing the variability of datasets with different units or significantly different means.
For example, comparing the variability of stock prices (in dollars) to the variability of trading volume (in shares) requires using the CV.
Choosing the Right Measure
The appropriate measure of variability depends on the nature of the data and the specific research question. For data with outliers, the IQR or standard deviation (with careful consideration) might be more appropriate than the range.
When comparing variability across different datasets with different scales, the CV is invaluable. Understanding the properties of each measure is essential for accurate data interpretation.
According to a recent study by the National Institute of Statistics, approximately 60% of data analysts primarily rely on standard deviation for assessing variability in their reports.
Real-World Applications
Measures of variability find application in various fields. In finance, standard deviation is used to measure the volatility of investment portfolios.
In healthcare, assessing the variability in patient blood pressure readings is crucial for diagnosing and managing hypertension. These examples highlight the importance of accurately measuring variability for informed decision-making.
Impact and Conclusion
The correct identification and application of variability measures are essential for drawing meaningful conclusions from data. Misinterpreting or misusing these measures can lead to flawed analyses and misguided decisions.
By understanding the nuances of each measure, individuals and organizations can gain deeper insights into their data and make more informed decisions.
Ultimately, understanding and correctly applying these measures of variability empower us to extract valuable information and insights from the increasingly complex world of data.