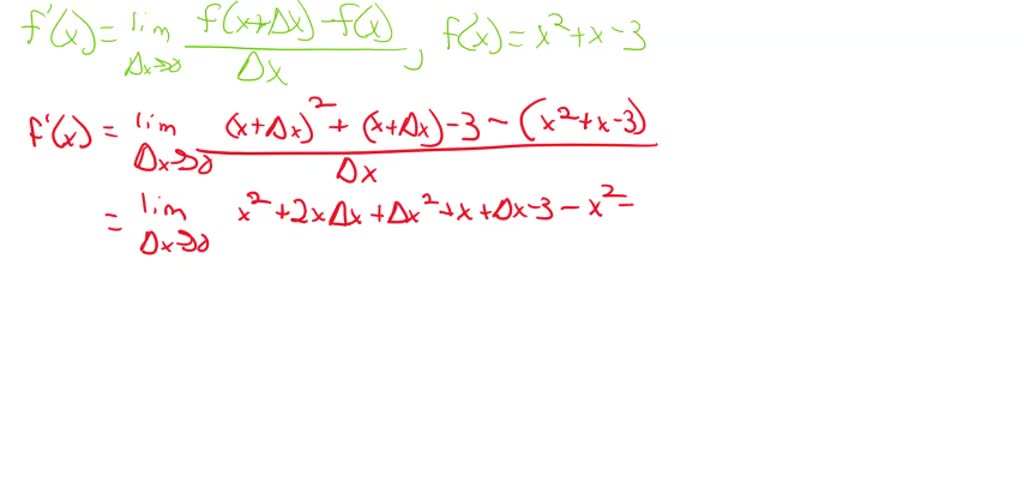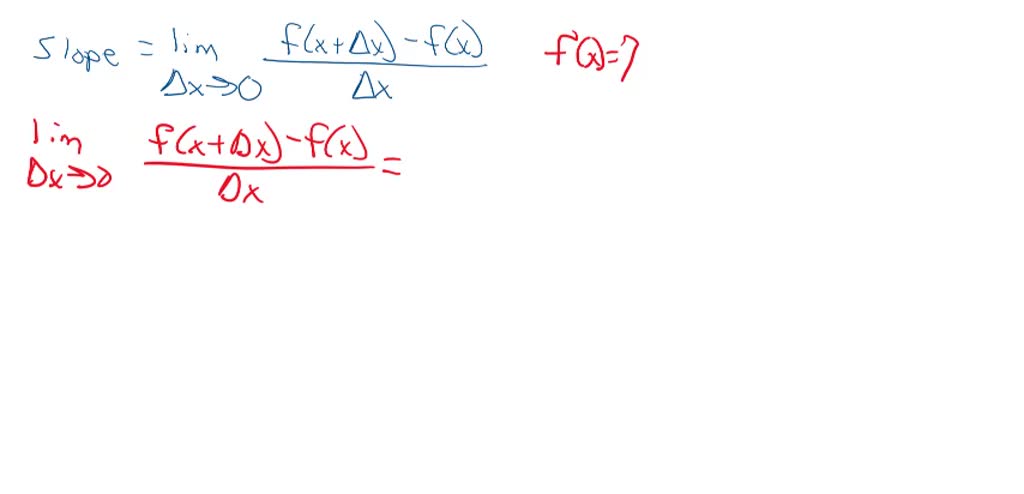Finding The Derivative By The Limit Process
Okay, picture this: you're at a ridiculously fun carnival. You've spotted the ultimate roller coaster, the "Deriva-Doom," known for its insane drops and loops.
You're not interested in riding, though. You're an engineer! You want to know exactly how steep the first drop is at any given point. You want to calculate the slope of that curve!
The Problem: Curves Are Tricky!
Finding the slope of a straight line is easy. Rise over run, right? But the Deriva-Doom's drop? It's curvy! How do you even begin to calculate the slope of a curve?
That’s where our friend, the limit process, comes to the rescue. Think of it as a mathematical magnifying glass.
Getting Closer... and Closer...
Imagine drawing a line between two points on the drop. It gives you a rough idea of the slope, but it’s not very accurate. Let's call this line the "secant" line.
Now, imagine moving the second point closer and closer to the first one. The secant line starts to look more and more like the curve itself right at that first point. It's like zooming in on a picture until it becomes perfectly clear.
Keep shrinking the distance between the points, making it ridiculously small. Infinitesimally small, some might say! This is where the magic happens.
The Limit: A Mathematical Tightrope Walk
We are trying to make the distance so small that it is virtually zero, but we don’t actually let it *be* zero. Think of it like getting really, really close to the edge of a cliff, but never quite falling off. This "getting really, really close" is the limit.
Finding the limit is like walking a tightrope. You're edging towards zero distance, but if you actually hit zero, the whole thing collapses. Division by zero is the mathematical equivalent of falling off that cliff!
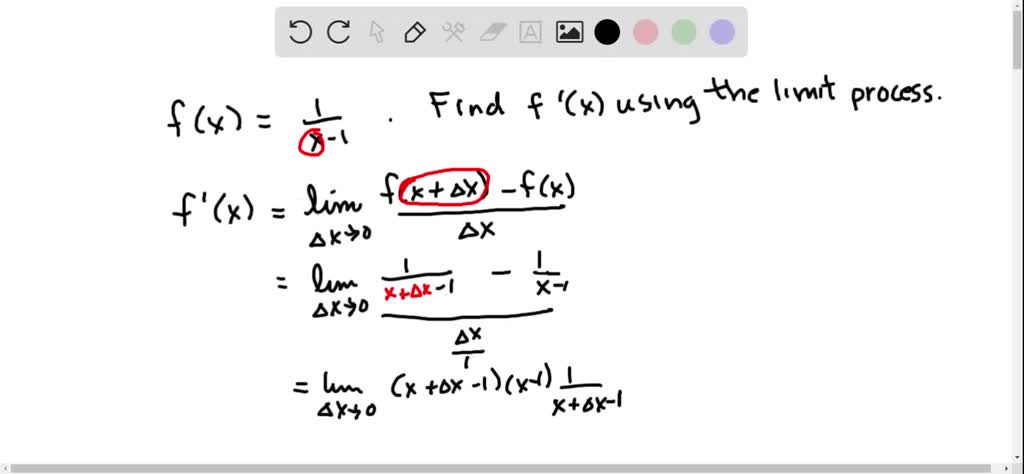
The limit of the slope of the secant line, as the distance between the points approaches zero, is the slope of the curve at that exact point. That’s the derivative!
Deriva-Doom Secrets Revealed!
So, you've used the limit process to find the slope of the Deriva-Doom's drop at a specific point. Now you can calculate exactly how thrilling (or terrifying!) that moment will be.
This process is used for all kinds of things. Engineering, physics, even economics! It's about finding the instantaneous rate of change, how things are changing *right now*.
Next time you see a curve, remember the Deriva-Doom. Remember the thrill of getting infinitely close, but never quite reaching zero. Remember the limit process, a tiny mathematical magnifying glass that unlocks the secrets of curves.
The limit process is not just a calculation; it's a way of thinking. It's a way of understanding how things change, not just in big leaps, but in tiny, almost imperceptible increments.
Pretty cool, huh?