A Consistent System Has How Many Solutions
A nationwide math crisis has been declared following the revelation that the fundamental question, "A consistent system has how many solutions?" is triggering widespread confusion and impacting standardized test scores. Educators and policymakers are scrambling to address the knowledge gap that threatens academic progress.
The question probes understanding of linear algebra, a cornerstone of higher mathematics and critical for STEM fields. Failure to grasp this concept is not merely an academic issue; it impacts students' ability to reason logically and solve complex problems across disciplines.
The Immediate Impact
Standardized test scores, particularly in mathematics, have seen a noticeable decline across multiple states. This drop is attributed, in part, to the difficulty students are having with questions directly related to linear systems and their solutions.
Preliminary data indicates that the performance dip is most pronounced amongst high school juniors and seniors. The College Board, responsible for the SAT, acknowledges a slight decrease in the average math score but refrains from directly linking it to the 'consistent system' question.
Educators report increased student anxiety and frustration during algebra lessons. The seemingly simple question, "A consistent system has how many solutions?" is proving surprisingly elusive.
What Defines a Consistent System?
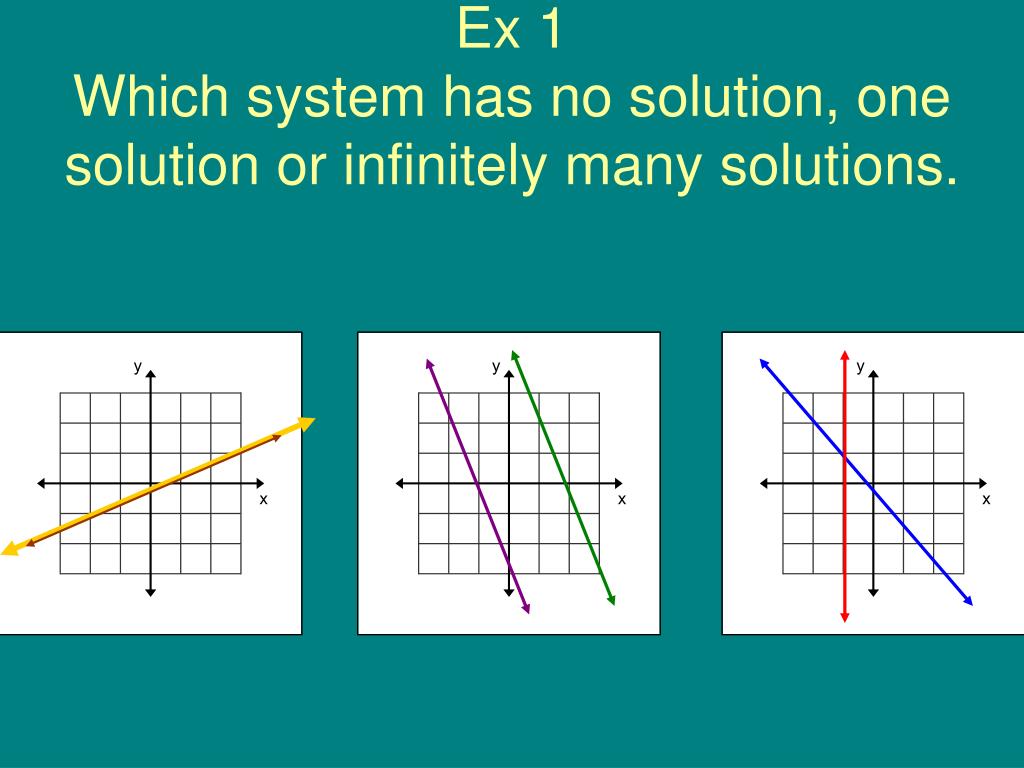
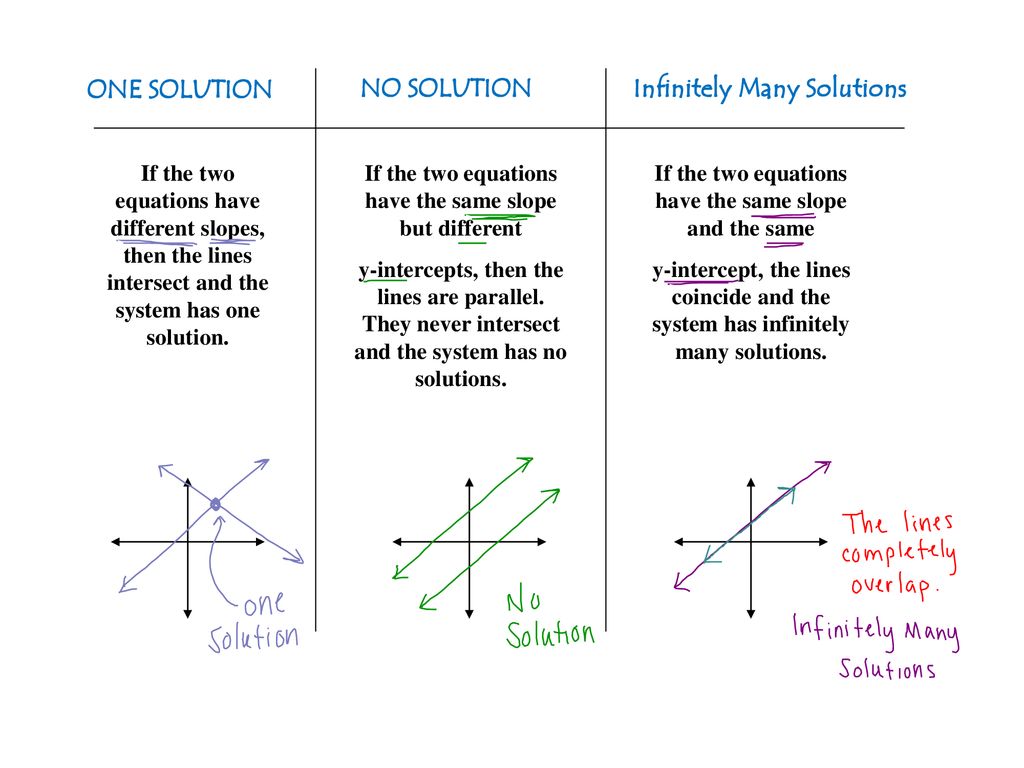
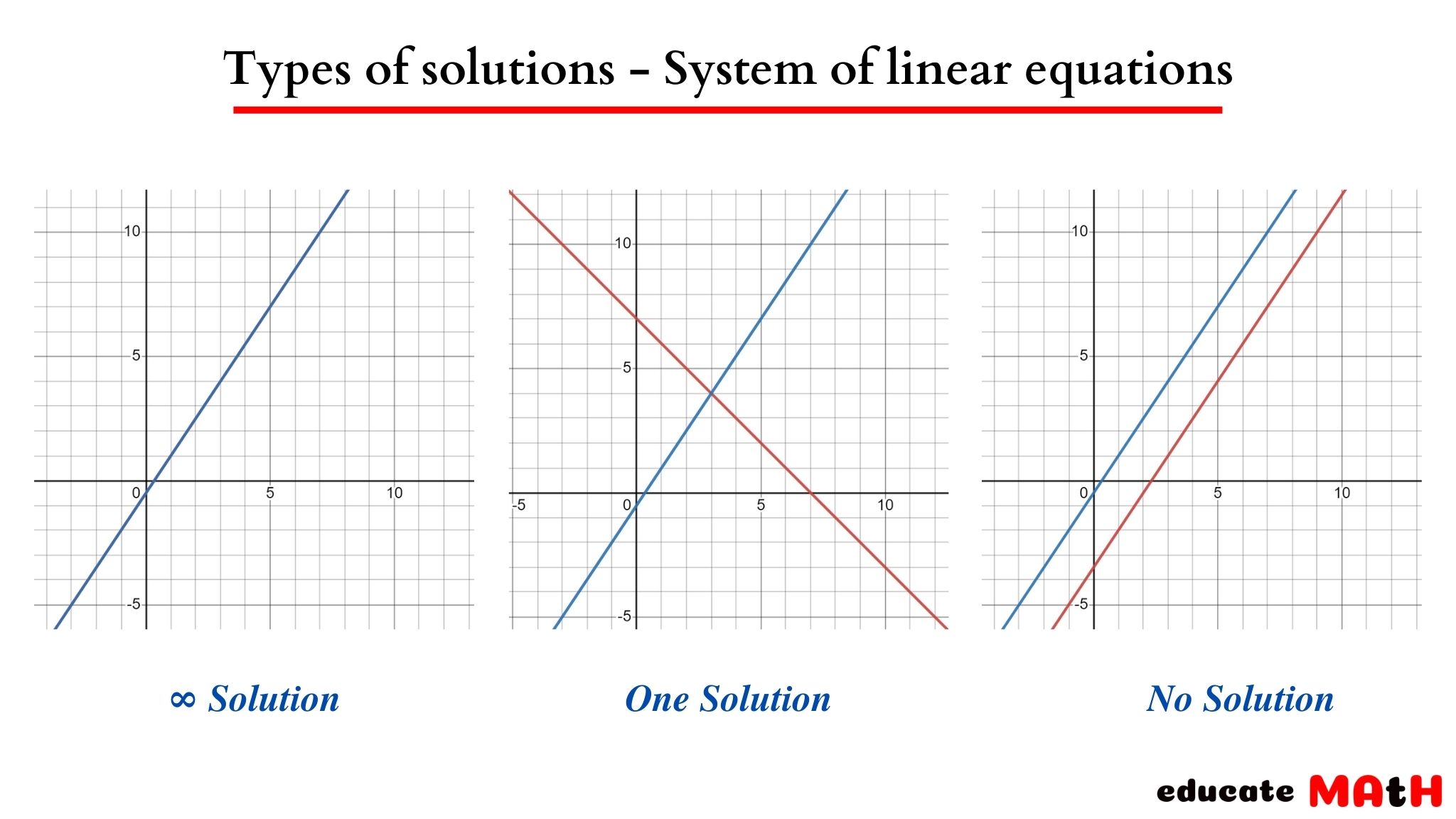
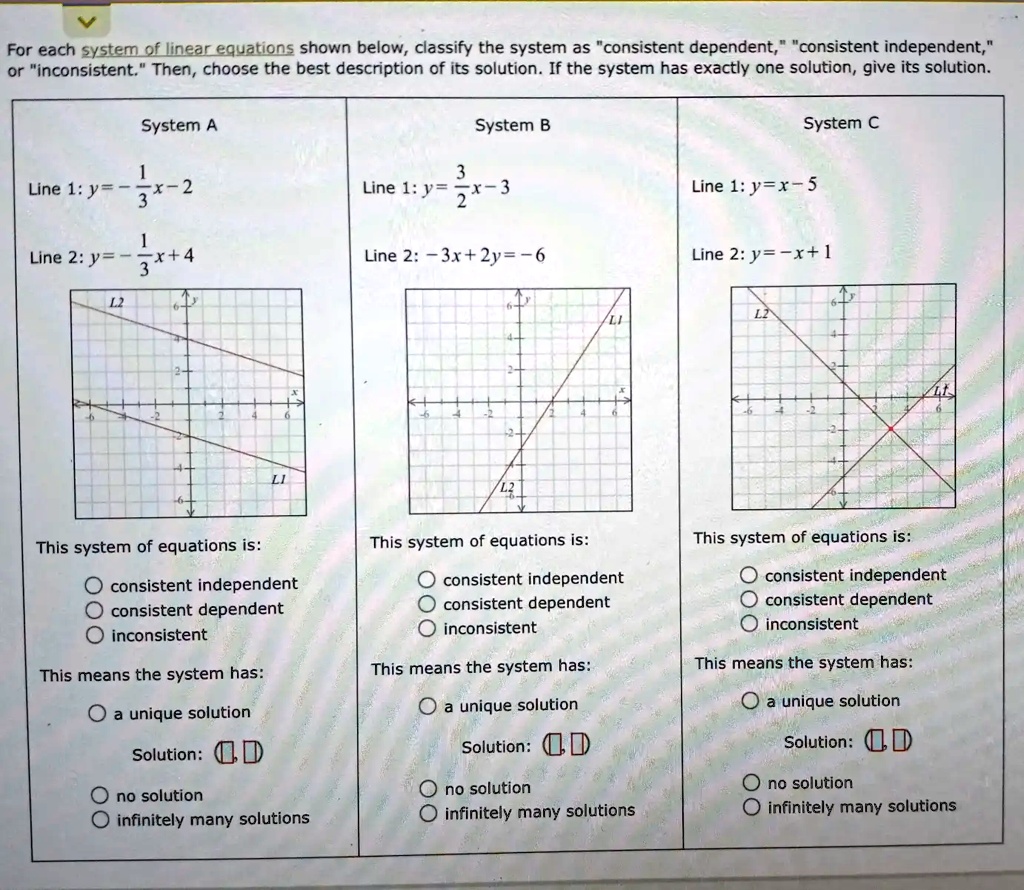
A consistent system of equations is one that has at least one solution. This basic definition is where the confusion often starts.
A consistent system can have one unique solution, where the lines (in a two-variable system) intersect at a single point. Alternatively, it can have infinitely many solutions, represented graphically by overlapping lines.
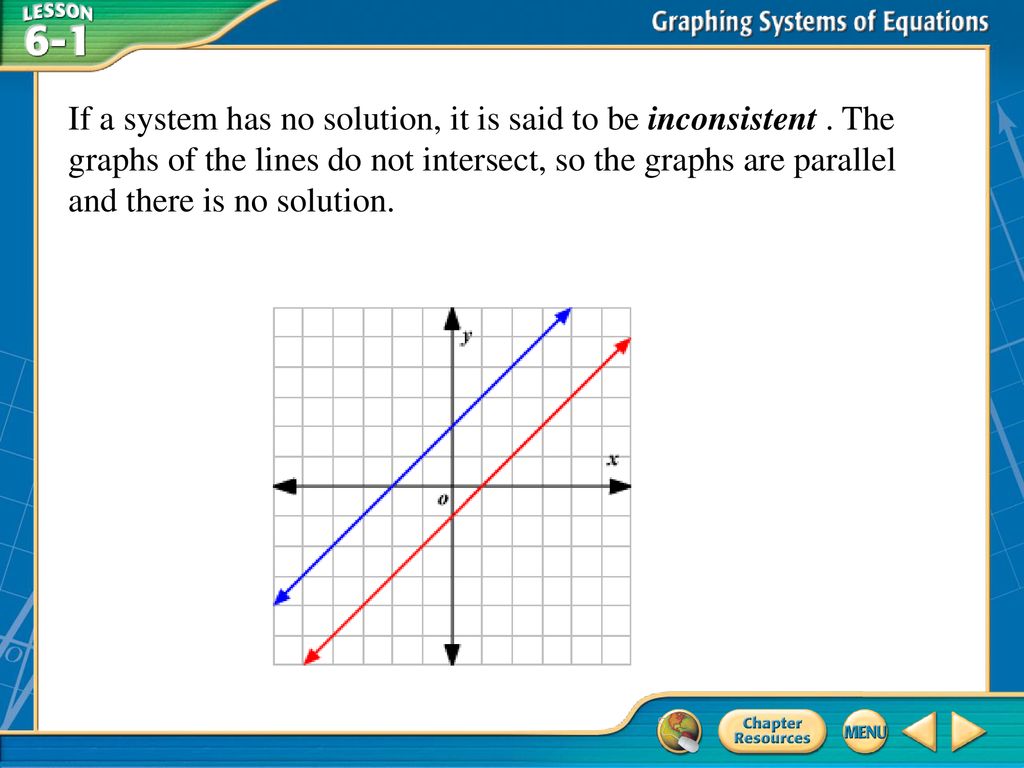
The crucial distinction lies between consistent and inconsistent systems. An inconsistent system, by contrast, has no solution.
The Role of Teachers and Curriculum
Teacher training programs are under scrutiny. Many question whether current educators are adequately equipped to teach linear algebra concepts effectively.
Curriculum design is also being reassessed. Experts are calling for a more intuitive and hands-on approach to teaching linear systems, rather than rote memorization of formulas.
Dr. Anya Sharma, a professor of mathematics education at MIT, stated: "We need to move beyond abstract equations and show students the real-world applications of linear algebra. This will make the concepts more engaging and easier to grasp."
Who is Affected?
The impact spans various educational levels, from secondary schools to universities. Students pursuing STEM degrees are particularly at risk if they lack a solid foundation in linear algebra.
Beyond academia, professions requiring analytical skills – engineering, finance, and data science – are also indirectly affected. Employers are concerned about the preparedness of recent graduates.
Parents are also expressing concern. Many are seeking additional tutoring and resources to help their children overcome this hurdle.
The Search for Solutions
The National Council of Teachers of Mathematics (NCTM) is developing supplementary materials and workshops for teachers. These resources aim to clarify the concept of consistent systems and provide effective teaching strategies.
Several universities are offering free online courses on linear algebra for high school students. These initiatives seek to bridge the knowledge gap and provide access to quality education.
The Department of Education is considering funding initiatives focused on improving math literacy. This includes providing grants to schools for professional development and curriculum enhancement.
Next Steps and Ongoing Developments
A national task force composed of educators, mathematicians, and policymakers has been formed. Its goal is to develop a comprehensive plan to address the math crisis.
The task force is expected to release its recommendations within the next three months. These recommendations will likely include changes to teacher training, curriculum standards, and assessment methods.
In the meantime, parents and students are encouraged to seek out additional resources and support. Understanding the fundamentals of linear algebra is essential for academic and professional success.
