Common Factors Of 24 And 28

In the seemingly abstract world of mathematics, seemingly simple concepts often hold profound implications. At the heart of number theory lies the notion of common factors – numbers that divide evenly into two or more other numbers. While the common factors of 24 and 28 might appear trivial at first glance, understanding them unlocks fundamental principles that underpin various fields, from cryptography to computer science.
This article delves into the common factors of 24 and 28, examining their significance, methods for finding them, and their practical applications. It aims to illuminate the beauty and utility hidden within this elementary mathematical concept.
Understanding Factors and Common Factors
A factor of a number is an integer that divides evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Factors are crucial for understanding divisibility and prime factorization.
Common factors, conversely, are the factors that two or more numbers share. Identifying these common divisors is essential for simplifying fractions, solving algebraic equations, and understanding number relationships.
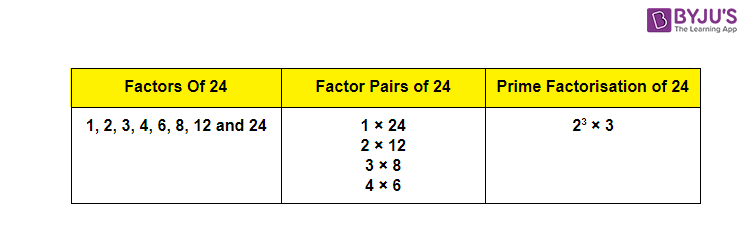
Finding the Factors of 24 and 28
To determine the common factors of 24 and 28, we must first list all the factors of each number individually. The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
The factors of 28 are 1, 2, 4, 7, 14, and 28. A systematic approach ensures that no factor is missed.
Identifying Common Factors of 24 and 28
By comparing the lists of factors for 24 and 28, we can identify the numbers that appear in both lists. The common factors of 24 and 28 are 1, 2, and 4.
Therefore, 1, 2, and 4 are the only whole numbers that divide both 24 and 28 without leaving a remainder.
The Greatest Common Factor (GCF)
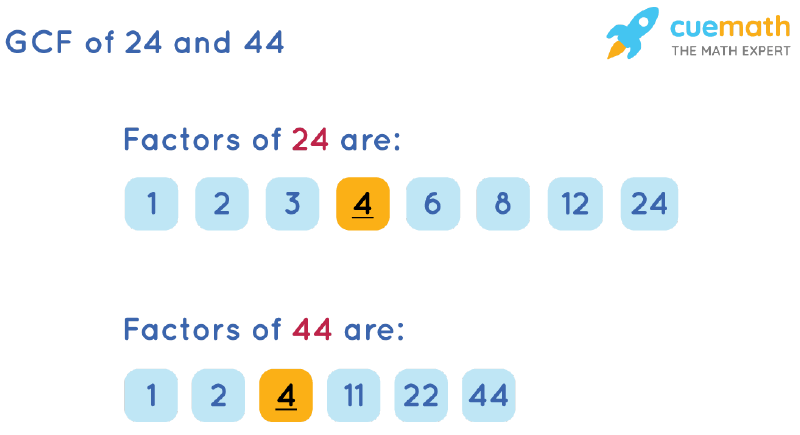
Among the common factors of two or more numbers, the largest is known as the greatest common factor (GCF). In the case of 24 and 28, the GCF is 4.
The GCF is a fundamental concept in mathematics, particularly in simplifying fractions and solving problems involving proportions. It represents the largest shared divisor of the given numbers.
Methods for Finding the GCF
Several methods exist for determining the GCF, including listing factors, prime factorization, and the Euclidean algorithm. The listing factors method, as demonstrated above, is effective for smaller numbers.
Prime factorization involves breaking down each number into its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power they appear in either factorization. For example, 24 = 23 x 3 and 28 = 22 x 7; the GCF is 22 = 4.
The Euclidean algorithm is an iterative method that involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is zero. The last non-zero remainder is the GCF.
Applications of Common Factors and GCF
The concepts of common factors and GCF are not confined to the realm of pure mathematics. They have significant practical applications in various fields.
In simplifying fractions, the GCF is used to reduce a fraction to its simplest form. For example, the fraction 24/28 can be simplified by dividing both the numerator and denominator by their GCF, 4, resulting in the simplified fraction 6/7.
Common factors and GCFs play a role in determining the optimal size of groups or arrangements when dealing with limited resources or specific constraints. This is often used in resource allocation and logistical planning.
Beyond Basic Arithmetic
The principles underlying common factors extend to more advanced mathematical concepts. They are fundamental to understanding number theory and abstract algebra.
In cryptography, understanding the properties of numbers, including their factors, is crucial for designing secure encryption algorithms. The security of many cryptographic systems relies on the difficulty of factoring large numbers.
In computer science, common factors are used in data compression algorithms to identify patterns and redundancies in data. They are also used in hashing algorithms to distribute data evenly across a hash table.
Looking Ahead
The exploration of common factors of 24 and 28 underscores the significance of seemingly basic mathematical concepts. As technology advances and complex systems emerge, the foundational principles of number theory become increasingly relevant.
Future research could focus on developing more efficient algorithms for finding common factors and GCFs of extremely large numbers. The efficiency and security of modern cryptographic systems depend on such advancement.
By continuing to explore and understand the properties of numbers, we can unlock new possibilities and solve complex problems in a variety of fields. The journey begins with understanding the simple concepts, like the common factors of 24 and 28.