Common Factors Of 9 And 12

Imagine a sunny afternoon, kids gathered around a table, colorful blocks scattered about. They're not just playing; they're discovering the hidden connections between numbers, unlocking mathematical secrets with every arrangement of those little squares. The excitement is palpable as they realize how certain numbers, like 9 and 12, share a special bond.
This bond, the shared factors of numbers like 9 and 12, isn't just a dry mathematical concept. It's a fundamental building block for understanding more complex ideas, from simplifying fractions to solving real-world problems. Unveiling these common factors illuminates the elegant structure that underlies the often intimidating world of mathematics.
The Foundation: What are Factors?
Before diving into the specific relationship between 9 and 12, let's establish a solid understanding of what factors are. In simple terms, a factor of a number is any whole number that divides evenly into it, leaving no remainder. Think of it as fitting puzzle pieces perfectly into a frame.
For example, the factors of 6 are 1, 2, 3, and 6 because 6 ÷ 1 = 6, 6 ÷ 2 = 3, 6 ÷ 3 = 2, and 6 ÷ 6 = 1. Each division results in a whole number, solidifying these as factors.
Delving into the Factors of 9
Now, let's examine the factors of 9. What numbers divide evenly into 9? The answer reveals itself through simple division: 1, 3, and 9.
1 is always a factor of any number, because any number divided by 1 is itself. 3 is a factor because 9 ÷ 3 = 3. And of course, 9 is a factor of itself, as 9 ÷ 9 = 1.
Exploring the Factors of 12
Next, we turn our attention to 12. Finding its factors involves a similar process of identifying numbers that divide evenly. Here, the factors are: 1, 2, 3, 4, 6, and 12.
We can see that 12 is divisible by 1, 2, 3, 4, 6, and itself. This set represents all the whole numbers that "fit" perfectly into 12.
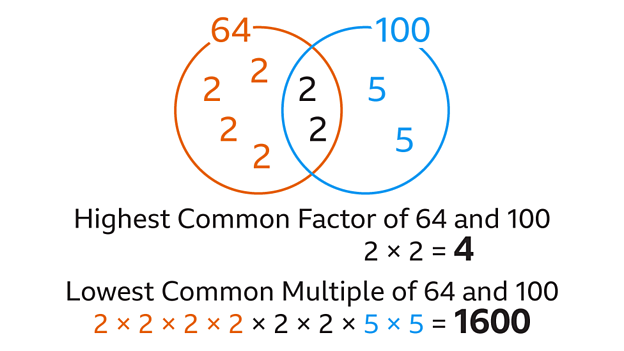
The Intersection: Common Factors Revealed
Here's where the magic happens. Now that we know the factors of both 9 and 12, we can identify the numbers they share, their common factors. By comparing the two lists, we can see that the common factors of 9 and 12 are 1 and 3.
Both 9 and 12 can be divided evenly by 1 and 3. This shared divisibility forms the basis of their connection.
The Significance of the Greatest Common Factor (GCF)
Among the common factors, there's one that reigns supreme: the Greatest Common Factor, or GCF. The GCF is the largest number that divides evenly into both numbers. In the case of 9 and 12, the GCF is 3.
The GCF is a powerful tool with numerous applications. From simplifying fractions to solving algebraic equations, understanding the GCF unlocks efficiencies and provides elegant solutions.
Applications in the Real World
The concept of common factors extends far beyond the classroom. It's a principle woven into the fabric of our daily lives. Think about sharing a pizza or dividing tasks among a group.
Consider arranging 9 chairs in rows. You could have one row of 9 chairs or three rows of 3 chairs. Similarly, 12 chairs can be arranged in one row of 12, two rows of 6, three rows of 4, four rows of 3, or six rows of 2. The common factor 3 means both sets of chairs can neatly form groups of 3, with no chairs left over.
In fields like computer science and engineering, GCF is used for optimizing code and designing efficient systems. For instance, when allocating resources, the GCF helps in distributing them proportionally.
Beyond the Basics: Exploring Further
Understanding common factors opens doors to more advanced mathematical concepts. From prime factorization to least common multiples, the foundational knowledge gained from exploring factors provides a springboard for further learning. The National Council of Teachers of Mathematics (NCTM) emphasizes the importance of building strong number sense from an early age.
Exploring numbers isn't about memorizing rules. Instead, it's about fostering curiosity and encouraging exploration. By playing with numbers, kids discover the patterns and relationships that make mathematics so fascinating.
"Mathematics is, in its way, the poetry of logical ideas." - Albert Einstein
A Final Reflection
So, what might seem like a simple exercise – finding the common factors of 9 and 12 – reveals a deeper understanding of mathematical principles. It's not just about numbers; it's about relationships, connections, and the inherent logic that governs our world.
The next time you encounter numbers, take a moment to explore their hidden connections. You might be surprised at the beauty and complexity you uncover. These fundamental concepts are stepping stones toward understanding complex topics.


.webp)