How To Do Cross Product On Ti 84 Plus

For students navigating physics, engineering, and advanced mathematics, the Ti-84 Plus graphing calculator remains a ubiquitous tool. While the calculator is well-known for graphing functions and performing statistical calculations, its capabilities extend to vector algebra, including the crucial operation of the cross product.
Many students, however, are unaware that the Ti-84 Plus doesn’t have a built-in function specifically for calculating the cross product of two vectors. This article provides a step-by-step guide on how to effectively and accurately perform cross-product calculations using the calculator's matrix functions.
First, the vectors must be represented as matrices. A 3D vector, for example, v = (a, b, c), is represented as a 3x1 matrix.
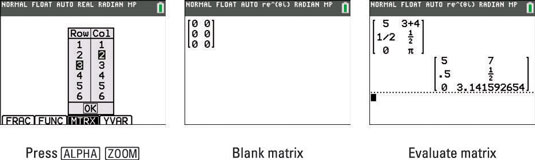
To input a matrix, press the "MATRIX" button, usually labeled as the inverse of the "x-1" key. Select "EDIT" and choose a matrix, such as "[A]", to edit.
Enter the dimensions of the matrix. For two 3D vectors, you’ll be working with 3x1 matrices.
Input the components of the first vector into the matrix. For example, if vector v = (2, -1, 3), enter 2, -1, and 3 into the first matrix, [A].
Repeat this process for the second vector. Enter the components of the second vector into another matrix, such as "[B]".
Now, define three new matrices to represent the unit vectors i, j, and k. These are (1, 0, 0), (0, 1, 0), and (0, 0, 1), respectively.
Store these as 3x1 matrices [C], [D], and [E]. This will simplify the calculation process.
The cross product, v x w, can be calculated using the determinant formula. This formula involves multiplying elements from the original vectors and the unit vectors.
Calculating Components
The x-component of the cross product is calculated as (b*wz - c*wy), where b and c are components of vector v and wy and wz are components of vector w. On the Ti-84 Plus, this translates to accessing the matrix elements and performing the calculation directly.
The y-component is calculated as (c*wx - a*wz). The z-component is calculated as (a*wy - b*wx).
Alternatively, use the det( ) function to calculate the determinant of a symbolically constructed matrix. This can be done by manually inputting the numbers into a 3x3 matrix to find the answer.
Manual Input Example
Press the "MATRIX" button and select "EDIT". Choose a new matrix, "[C]", and set its dimensions to 3x3.
Input the elements as follows: first row: i component, j component, k component; second row: components of vector v; third row: components of vector w.
Exit the matrix editor. Press "MATRIX" again, go to "MATH," and select "det(" to calculate the determinant of the matrix [C].
Press "ENTER" to execute the calculation. The result will be the determinant, which represents the cross product vector.
Although the Ti-84 Plus lacks a dedicated cross-product function, this method provides a workaround. It's a practical solution for students and professionals who rely on this calculator for their mathematical needs.