How To Find The Value Of An Angle

The world around us is built upon angles, from the architecture that defines our cities to the trajectories that guide spacecraft. Understanding how to determine the value of an angle is not merely an academic exercise; it's a fundamental skill that unlocks a deeper appreciation for geometry, physics, engineering, and countless other fields. The ability to accurately calculate angles is critical in navigation, construction, and even in creating realistic graphics for video games and movies.

This article will delve into the methods used to find the value of an angle. We'll explore diverse techniques, including using protractors, applying trigonometric functions, and leveraging geometric theorems. This exploration will provide a comprehensive guide suitable for anyone seeking to enhance their understanding of angular measurement, from students to professionals.

Measuring Angles with a Protractor

The most direct method for determining the value of an angle is by using a protractor. A protractor is a semicircular or circular instrument calibrated in degrees, typically ranging from 0° to 180° or 0° to 360°.

To measure an angle with a protractor, first align the center point of the protractor (the small notch or hole) with the vertex of the angle. Next, line up one side (or ray) of the angle with the 0° mark on the protractor.

Finally, observe where the other side of the angle intersects the protractor's scale. The reading at that point indicates the angle's measure in degrees.

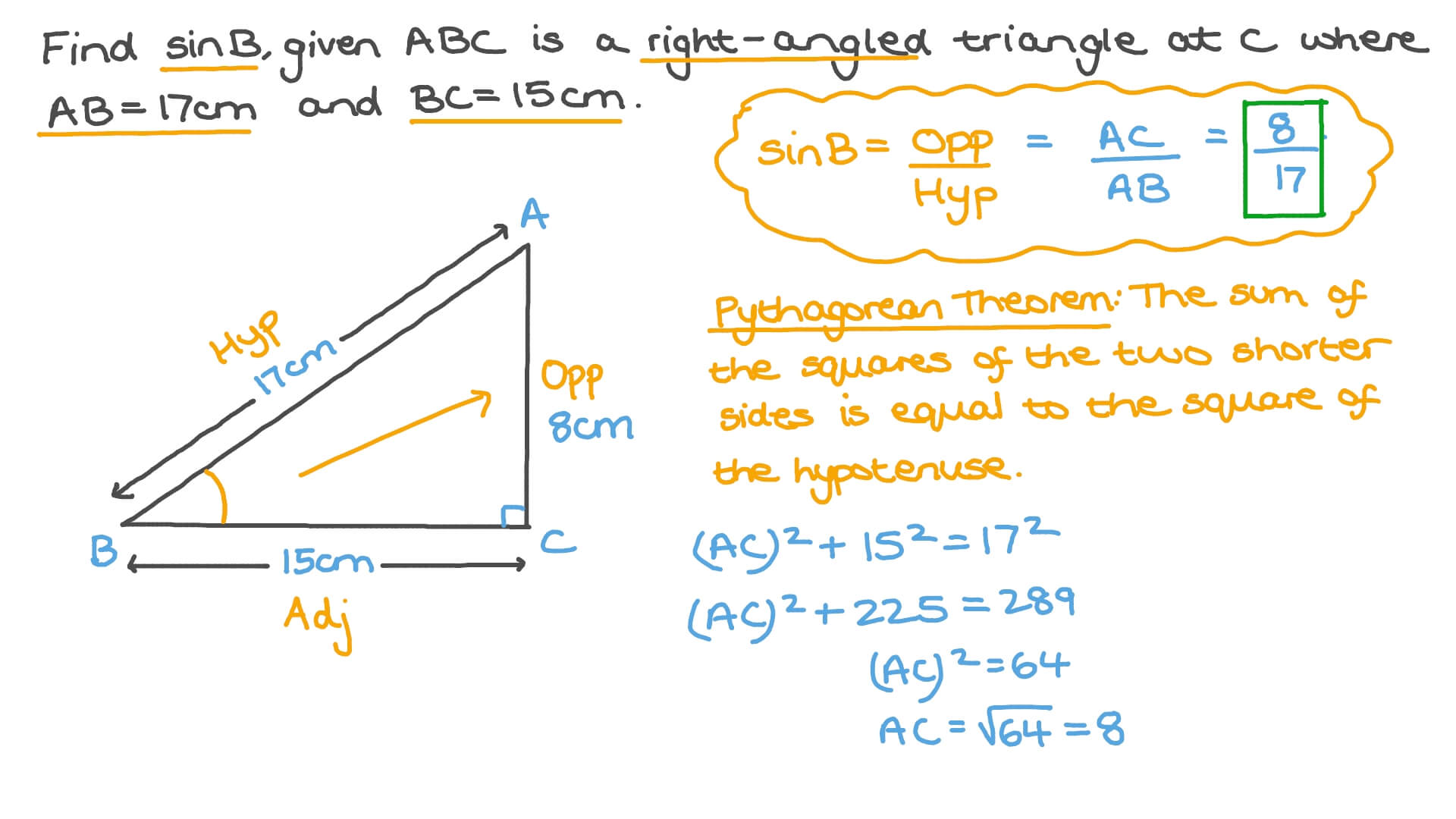
Trigonometric Functions: SOH CAH TOA

Trigonometric functions provide a powerful method for calculating angles within right triangles. The three primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan), often remembered by the mnemonic SOH CAH TOA.

SOH stands for Sine = Opposite / Hypotenuse. This means the sine of an angle is equal to the length of the side opposite the angle divided by the length of the hypotenuse.

CAH stands for Cosine = Adjacent / Hypotenuse. This indicates that the cosine of an angle is equal to the length of the side adjacent to the angle divided by the length of the hypotenuse.

TOA stands for Tangent = Opposite / Adjacent. This signifies that the tangent of an angle is equal to the length of the side opposite the angle divided by the length of the side adjacent to the angle.

If you know the lengths of two sides of a right triangle, you can use the inverse trigonometric functions (arcsin, arccos, arctan) to find the angle. For example, if you know the opposite and hypotenuse, you can use arcsin to find the angle: angle = arcsin(Opposite/Hypotenuse).

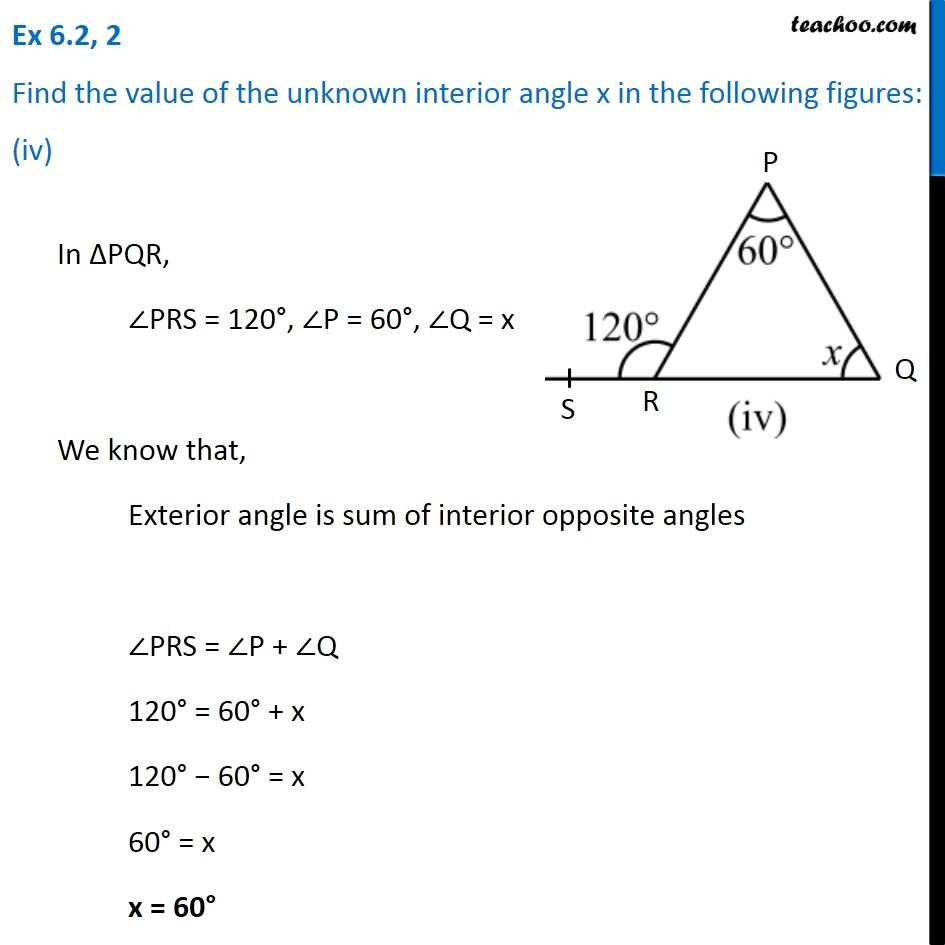
Geometric Theorems and Angle Relationships

Geometry provides several theorems and relationships that can be used to deduce the values of angles. One of the most fundamental is the fact that the sum of the angles in a triangle always equals 180°.

If you know the measures of two angles in a triangle, you can find the third angle by subtracting the sum of the known angles from 180°. This is a simple, yet powerful, technique.

Another important concept is that of supplementary and complementary angles. Supplementary angles are two angles whose sum is 180°, while complementary angles are two angles whose sum is 90°.

Knowing that two angles are supplementary or complementary allows you to find one angle if you know the other. Vertical angles (angles formed by two intersecting lines) are also equal, and alternate interior angles formed by a transversal intersecting parallel lines are congruent.

Example: Finding an Angle in a Parallelogram

Consider a parallelogram. Opposite angles in a parallelogram are equal, and consecutive angles are supplementary. If one angle in a parallelogram measures 60°, its opposite angle also measures 60°. Its adjacent angles (and the remaining angle) will each measure 120° (180° - 60° = 120°).

Using Computer Software and Calculators

Modern technology offers tools that greatly simplify angle calculation. Scientific calculators have built-in trigonometric functions and their inverses, allowing for quick and accurate angle determination.

Furthermore, specialized software like CAD (Computer-Aided Design) programs and geometry software packages allow for the precise measurement and manipulation of angles in various geometric shapes. These tools are essential for engineers, architects, and designers.

These programs often include features that automatically calculate angles based on given geometric constraints, reducing the possibility of human error. They are invaluable in creating accurate designs and models.

Advanced Techniques and Considerations

In more complex scenarios, finding the value of an angle may require a combination of techniques. This may involve using trigonometry in conjunction with geometric theorems or employing more advanced mathematical concepts like vectors and complex numbers.

For instance, in surveying, angles are often measured using theodolites, which provide highly accurate angular measurements. These measurements are then used in conjunction with other data to create maps and plans.

It's also crucial to be aware of potential sources of error when measuring angles. These can include parallax error when using a protractor, rounding errors when using trigonometric functions, and instrument errors when using measuring devices.

Conclusion: A Foundation for Understanding

Mastering the methods for finding the value of an angle is a fundamental skill with applications spanning numerous disciplines. From basic geometric constructions to advanced engineering design, the ability to accurately measure and calculate angles is essential for problem-solving and innovation.

Whether using a simple protractor, applying trigonometric functions, or leveraging sophisticated software, understanding the principles behind angular measurement empowers individuals to analyze and manipulate the world around them. As technology continues to advance, new tools and techniques will undoubtedly emerge, further enhancing our ability to understand and utilize angles in various applications.

The journey to master angle calculations is a continuous one, requiring practice, precision, and a solid understanding of the underlying principles. By embracing these challenges, one can unlock a deeper appreciation for the geometry that governs our world and unlock new possibilities in fields ranging from art and design to science and engineering.