Is 81 A Prime Number Or A Composite Number

In a world increasingly reliant on cryptography and data security, the seemingly simple question of whether a number is prime or composite takes on significant weight. Recent online debates and educational quizzes have brought renewed attention to the number 81, sparking discussions among students, educators, and even casual math enthusiasts. The core of the debate: is 81 a prime number, divisible only by 1 and itself, or a composite number, possessing additional divisors?
This article delves into the mathematical properties of 81 to definitively answer this question, exploring the concepts of prime and composite numbers, analyzing 81's divisors, and highlighting the importance of understanding these concepts in various fields. It aims to provide clarity and foster a deeper appreciation for number theory.
Understanding Prime and Composite Numbers
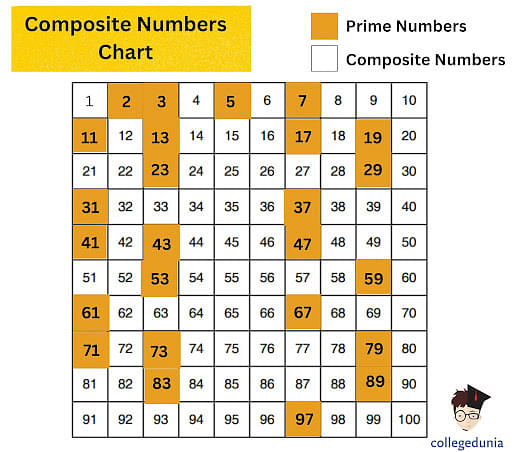
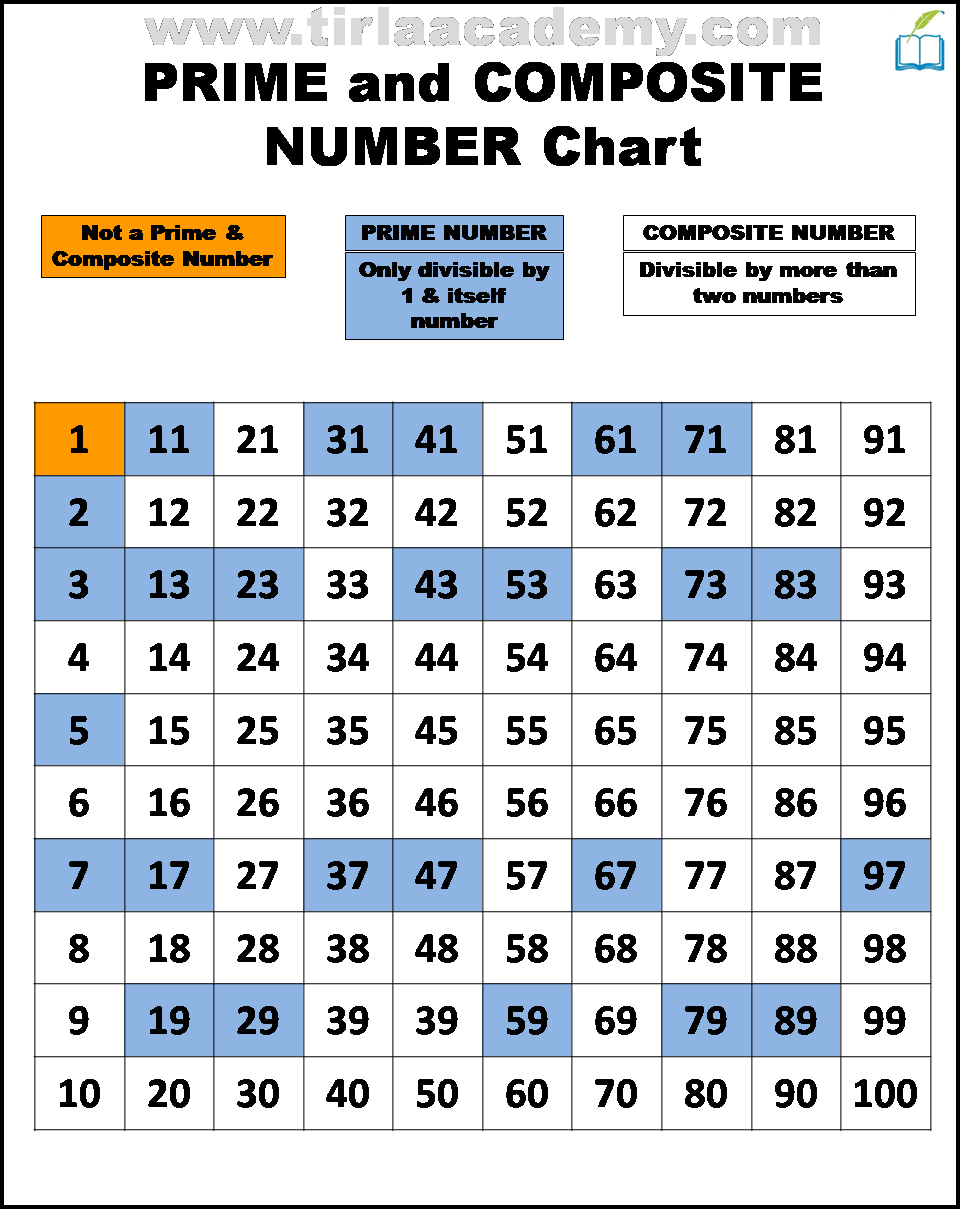
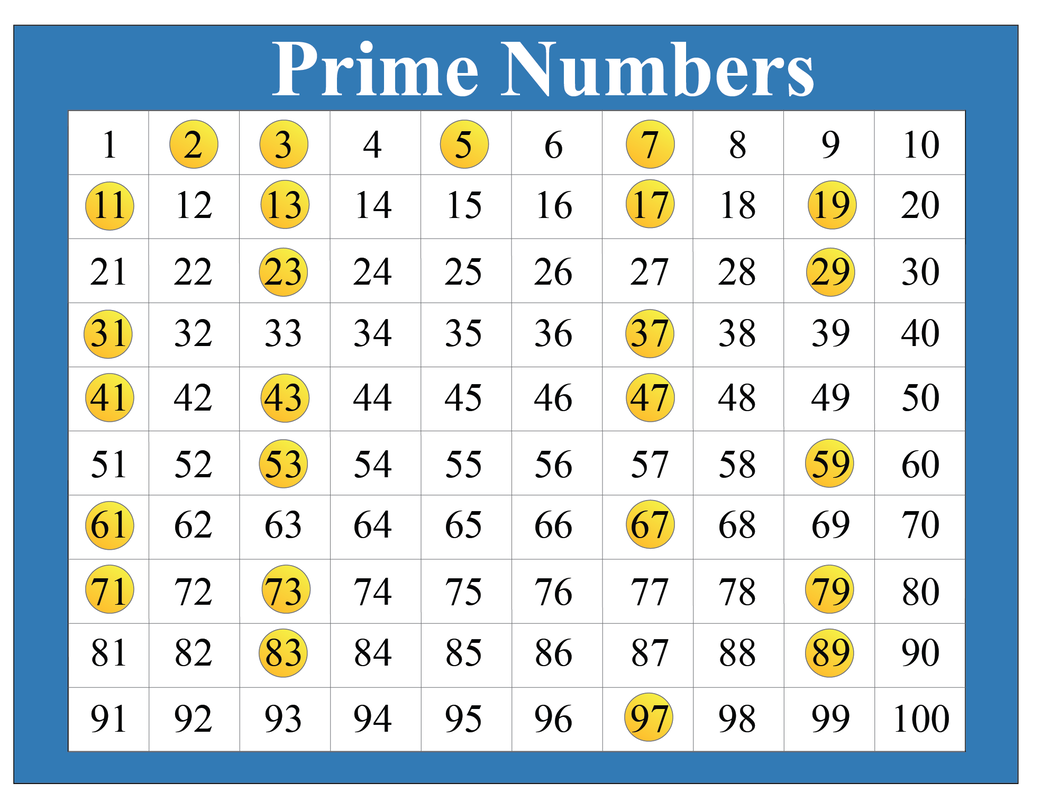
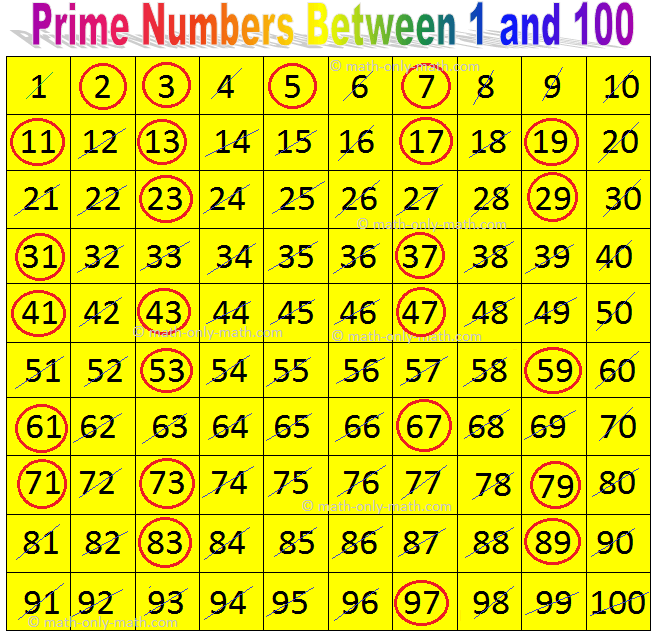
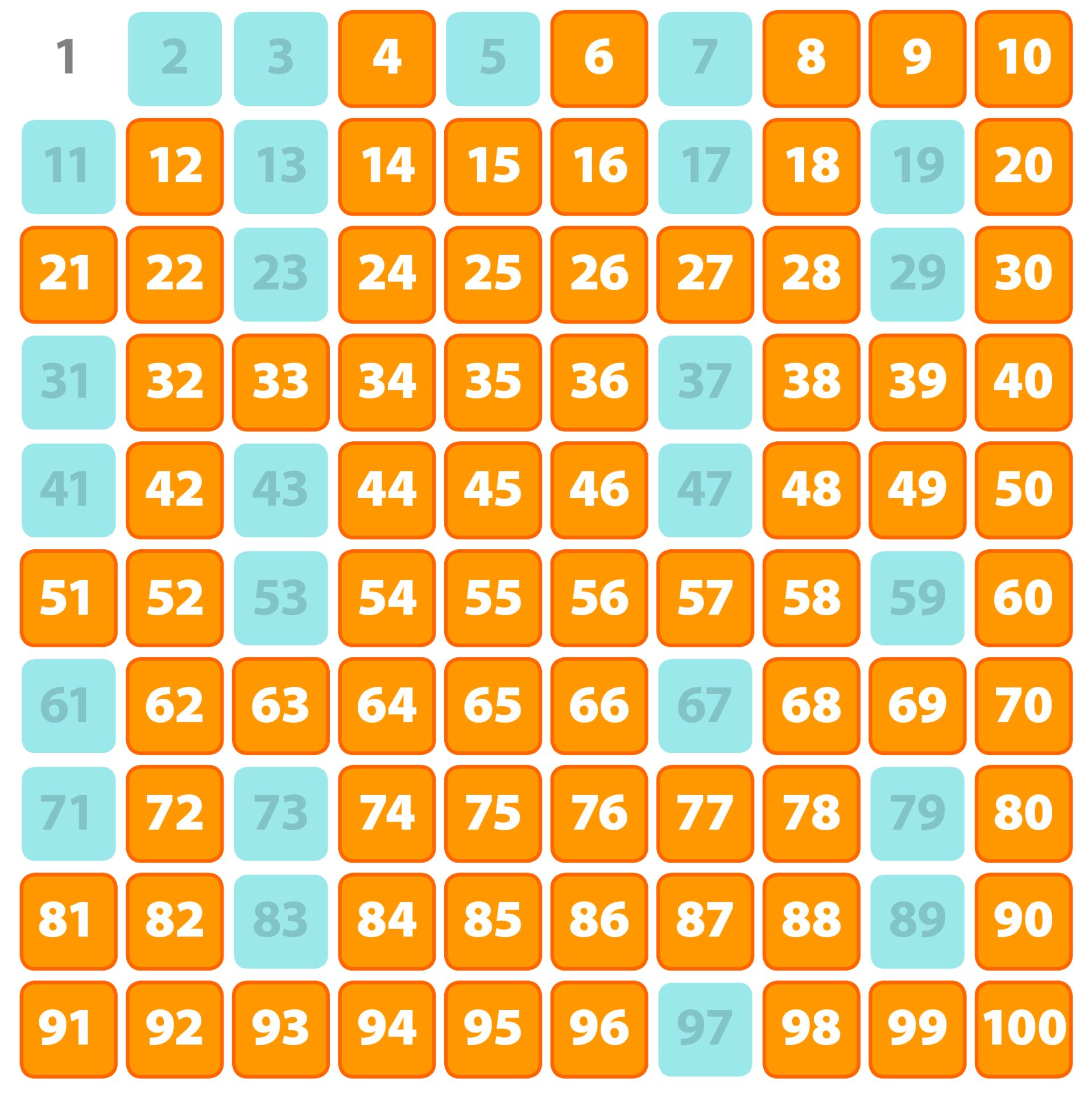
A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. A composite number, on the other hand, is a whole number greater than 1 that has more than two divisors.
In essence, composite numbers can be formed by multiplying two smaller whole numbers. Understanding the distinction between prime and composite numbers is fundamental to number theory and crucial for cryptographic algorithms.
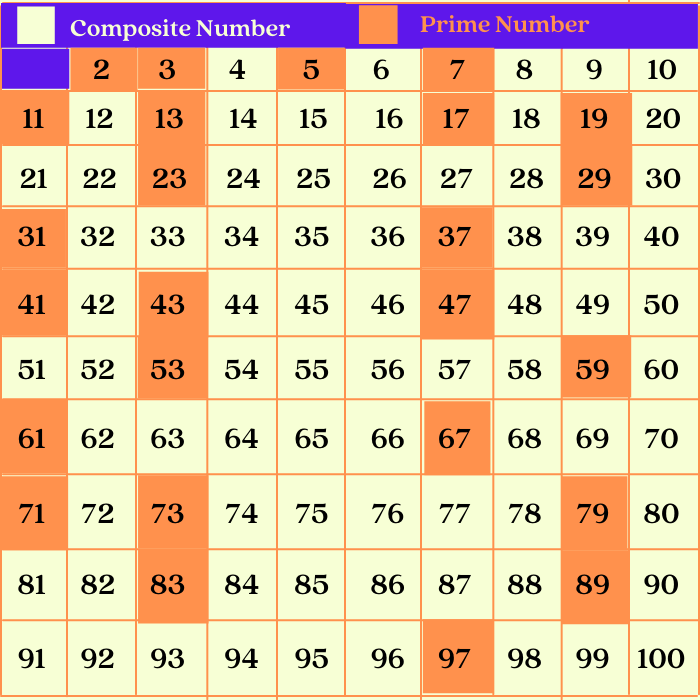
Analyzing the Divisors of 81
To determine whether 81 is prime or composite, we need to examine its divisors. A divisor of a number is a whole number that divides into it evenly, leaving no remainder. Let's systematically check the potential divisors of 81.
Identifying Factors
It's clear that 1 and 81 are divisors of 81. However, the presence of other divisors will definitively classify it as composite. The number 3 divides into 81: 81 / 3 = 27.
Furthermore, 9 also divides into 81: 81 / 9 = 9. Therefore, the divisors of 81 are 1, 3, 9, 27, and 81.
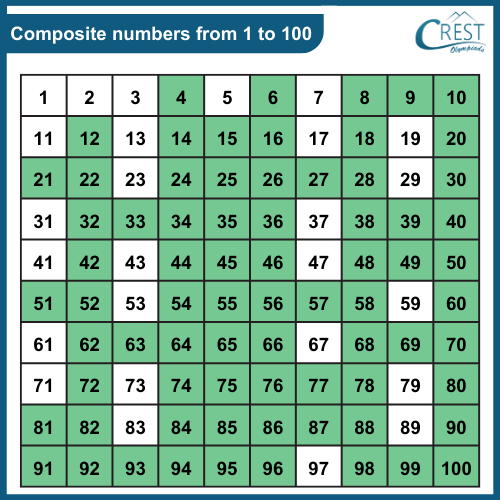
The Verdict: 81 is Composite
Since 81 has more than two divisors, it is definitively a composite number. This conclusion is based on the fundamental definition of prime and composite numbers. There is no ambiguity in this mathematical determination.
The Importance of Prime and Composite Numbers
The distinction between prime and composite numbers isn't merely an academic exercise; it has real-world implications. Prime numbers, in particular, play a vital role in cryptography, the science of secure communication.
Many encryption algorithms, such as RSA, rely on the difficulty of factoring large composite numbers into their prime factors. The security of these systems hinges on the fact that finding the prime factors of a very large composite number is computationally expensive.
Conversely, understanding composite numbers is essential for various mathematical operations and applications. From simplifying fractions to solving algebraic equations, the ability to identify and work with composite numbers is a core skill.
Addressing Common Misconceptions
The recent online discussions suggest some confusion about the definition of prime numbers. Some individuals may mistakenly believe that any odd number is prime. This is incorrect; while all prime numbers greater than 2 are odd, not all odd numbers are prime. 81 serves as a clear example of an odd number that is not prime.
Other misconceptions might arise from a lack of familiarity with divisibility rules. Remembering divisibility rules for common numbers like 3 and 9 can help quickly identify composite numbers.
Expert Opinions and Educational Resources
Mathematics educators consistently emphasize the importance of teaching prime and composite numbers from an early age. According to the National Council of Teachers of Mathematics (NCTM), understanding number theory concepts like prime factorization is crucial for developing mathematical reasoning and problem-solving skills.
Leading mathematicians and computer scientists agree on the critical role of prime numbers in modern technology.
"The security of the internet, to a significant extent, depends on the properties of prime numbers,"stated Dr. Alice Chen, a professor of cryptography at Stanford University.
Looking Ahead: The Future of Number Theory
Research in number theory continues to advance our understanding of prime numbers and their distribution. Mathematicians are still working on solving long-standing problems such as the Riemann Hypothesis, which relates to the distribution of prime numbers. These advancements not only deepen our theoretical knowledge but also have the potential to improve cryptographic algorithms and enhance data security.
The ongoing exploration of prime and composite numbers highlights the enduring relevance of fundamental mathematical concepts in the modern world. While the question of whether 81 is prime or composite may seem trivial at first glance, it underscores the importance of understanding these concepts for both academic and practical applications.
In conclusion, 81 is undeniably a composite number, possessing divisors beyond 1 and itself. This determination reinforces the fundamental principles of number theory and underscores the importance of mathematical literacy in an increasingly digital world.