Is 91 A Prime Number Or A Composite Number
In elementary mathematics education, a surprisingly common stumbling block emerges: the classification of the number 91. Is it a prime number, indivisible except by 1 and itself, or a composite number, harboring multiple factors? The answer, while seemingly straightforward to mathematicians, often eludes students, and even some adults, leading to confusion and a need for clarification.
This article aims to definitively answer the question: is 91 a prime or composite number? We will delve into the fundamental definitions of prime and composite numbers, explore the divisibility rules that can quickly identify factors, and ultimately, provide a clear and concise explanation for the classification of 91. This understanding is crucial not only for basic arithmetic but also for more advanced mathematical concepts like cryptography and number theory.
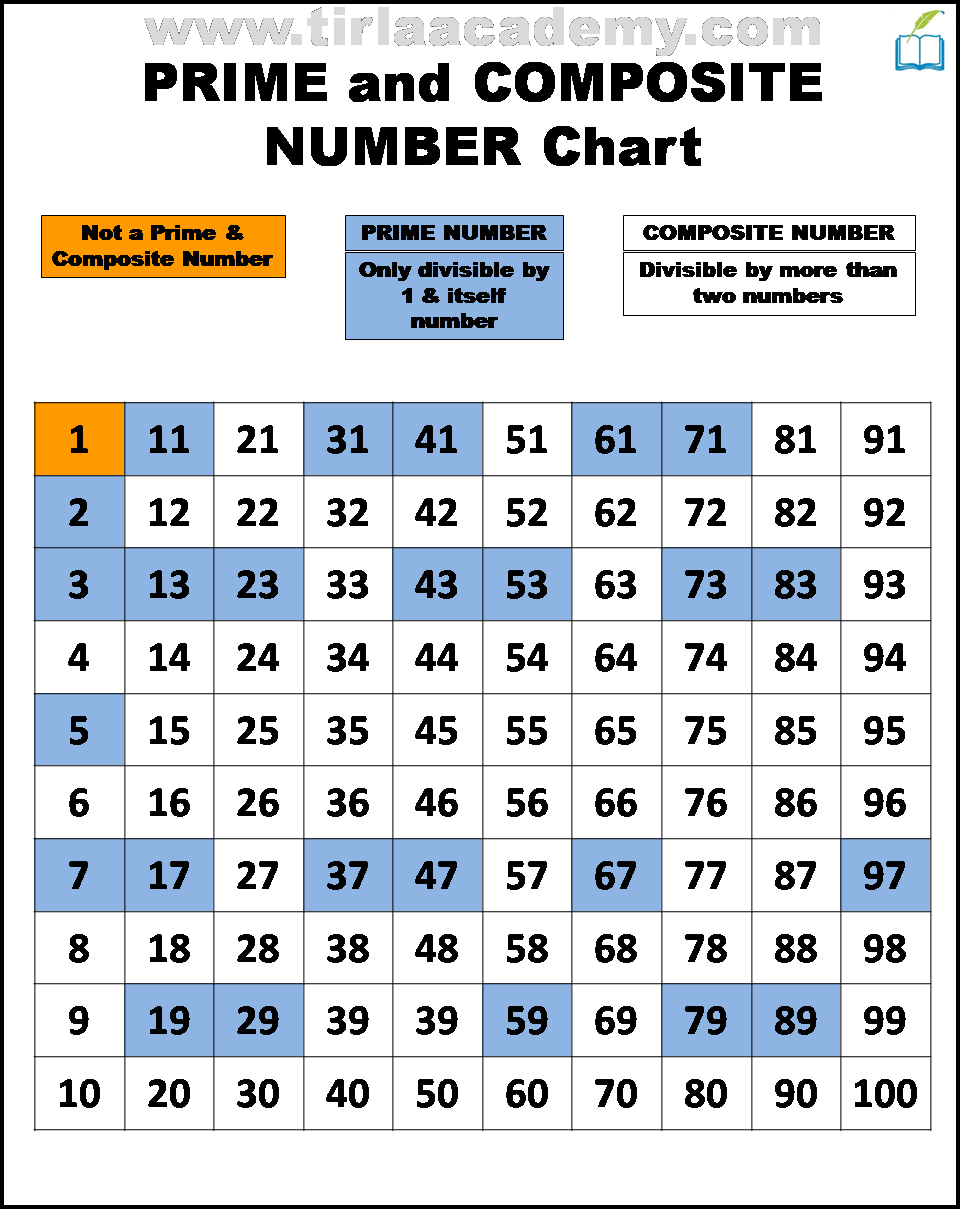
Prime Numbers: The Building Blocks
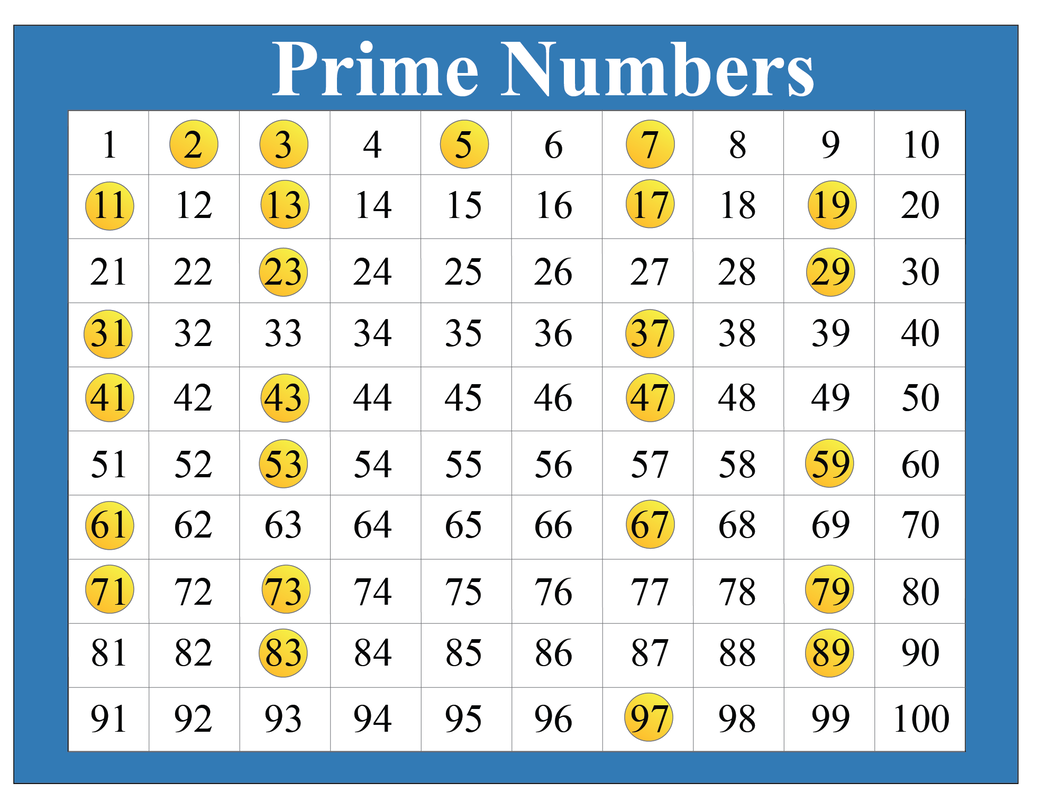
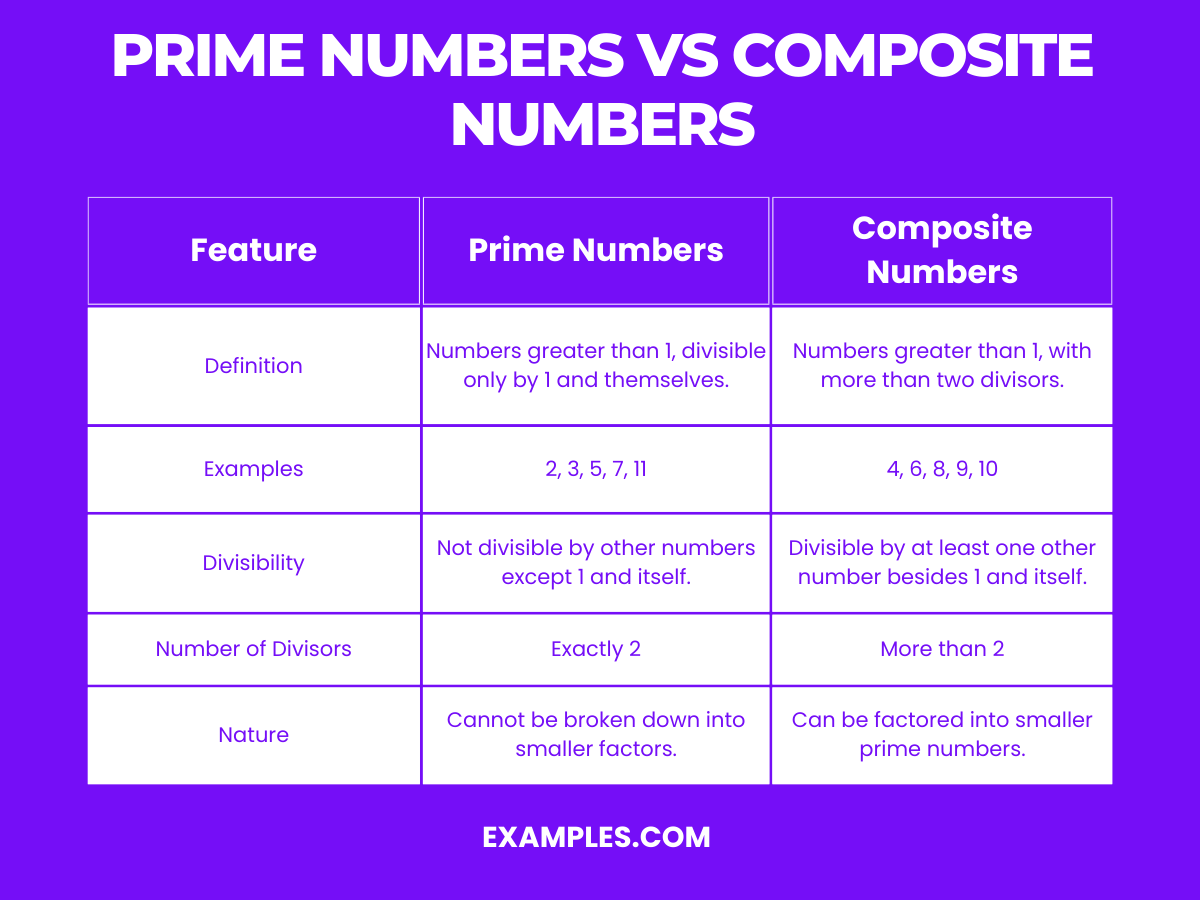
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, 13, and so on. Each of these numbers is only divisible by 1 and the number itself.
The significance of prime numbers lies in their role as the fundamental building blocks of all other natural numbers. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, up to the order of the factors.
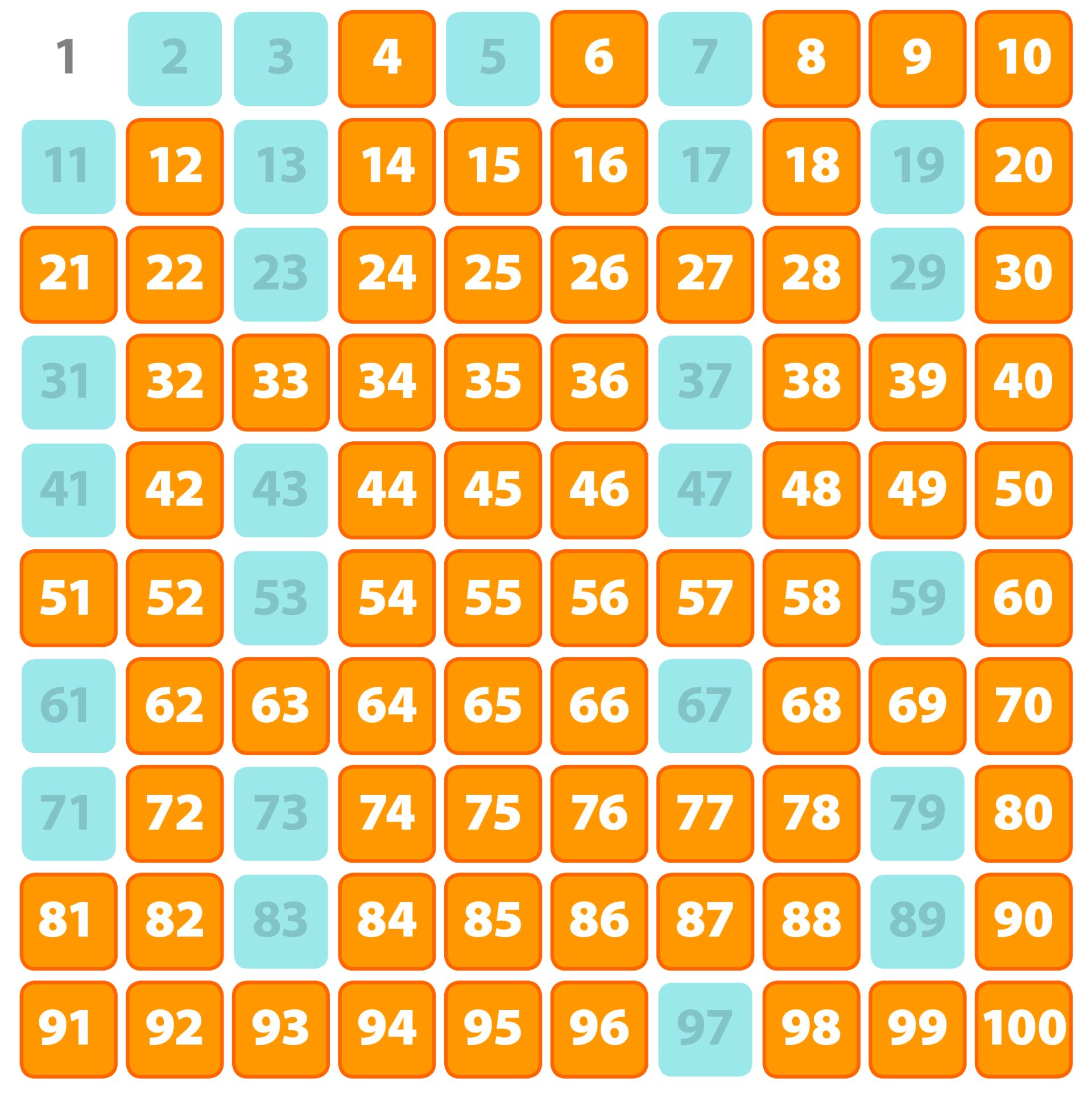
Composite Numbers: More Than Meets the Eye
A composite number, on the other hand, is a natural number greater than 1 that has at least one positive divisor other than 1 and itself. In simpler terms, a composite number can be divided evenly by a number other than 1 and itself.
Examples of composite numbers include 4, 6, 8, 9, 10, 12, and so on. Each of these numbers has multiple factors beyond 1 and itself. For instance, 6 is divisible by 1, 2, 3, and 6.
Divisibility Rules: A Quick Guide
Divisibility rules are shortcuts to determine whether a number is divisible by another number without performing long division. These rules are based on patterns in the digits of the number being tested.
Some common divisibility rules include: A number is divisible by 2 if its last digit is even. A number is divisible by 3 if the sum of its digits is divisible by 3. A number is divisible by 5 if its last digit is 0 or 5.
The divisibility rule for 7 is a bit more complex. One method involves doubling the last digit and subtracting it from the remaining truncated number; if the result is divisible by 7, then so was the original number.
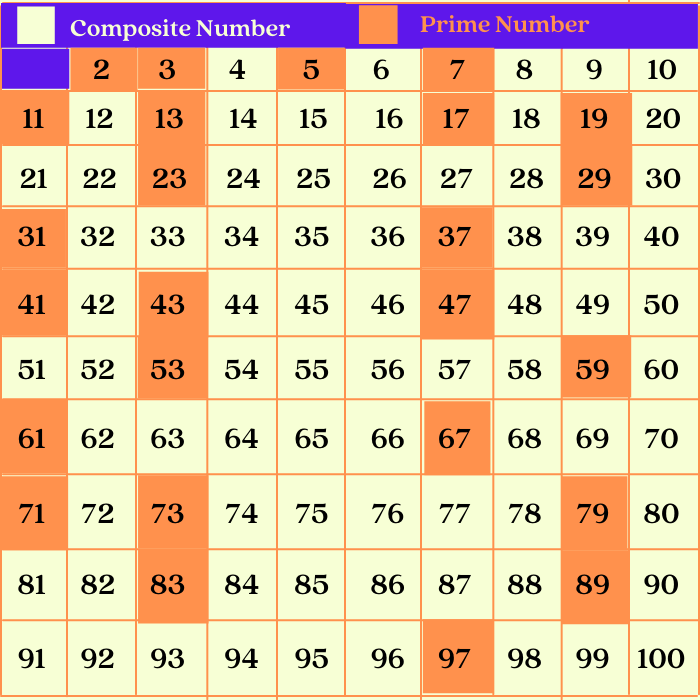
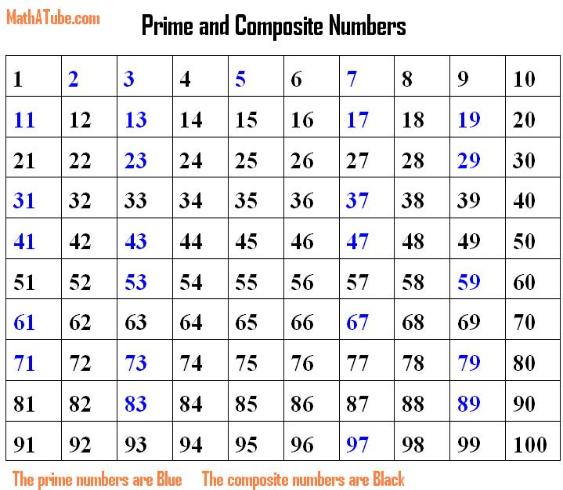
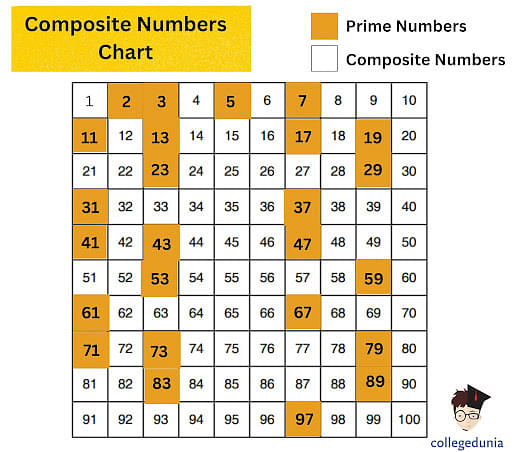
Analyzing 91: Prime or Composite?
Now, let's apply these principles to the number 91. At first glance, it might seem like a prime number, particularly for those less familiar with divisibility rules.
However, a closer look reveals that 91 is divisible by 7 and 13. Specifically, 91 = 7 x 13.
Therefore, since 91 has factors other than 1 and itself (namely, 7 and 13), it definitively qualifies as a composite number. This can be easily verified through simple division or using a calculator.
Why the Confusion?
The confusion surrounding the classification of 91 often stems from its relatively large size compared to commonly known prime numbers. Students may also not readily recognize 7 and 13 as factors without explicitly testing for them.
Furthermore, the absence of an obvious divisibility rule, like those for 2, 3, or 5, can mislead individuals into incorrectly assuming primality. The subtle divisibility by 7 often goes unnoticed.
Educational resources often emphasize the importance of mastering divisibility rules and practicing factorization to avoid such misconceptions. Regular practice can build number sense and improve the ability to quickly identify factors.
Real-World Applications
The distinction between prime and composite numbers is not merely an academic exercise. It has practical applications in various fields.
In cryptography, prime numbers are fundamental to secure communication. Algorithms like RSA (Rivest-Shamir-Adleman) rely on the difficulty of factoring large composite numbers into their prime factors to encrypt and decrypt sensitive information.
Understanding prime and composite numbers is also essential in areas like computer science, data compression, and even music theory. These concepts build the foundations for complex algorithms and processes.
Conclusion: 91 is Undeniably Composite
In conclusion, after careful analysis and application of the definition of prime and composite numbers, it is clear that 91 is a composite number. Its factors are 1, 7, 13, and 91.
This simple example highlights the importance of understanding fundamental mathematical concepts and employing effective problem-solving strategies. Mastering these principles allows for a deeper appreciation of the underlying structure of numbers and their applications in the real world.
Moving forward, educators should continue to emphasize the importance of number sense and provide ample opportunities for students to practice identifying prime and composite numbers. By fostering a solid foundation in basic arithmetic, we can empower individuals to navigate more complex mathematical challenges with confidence and understanding.
