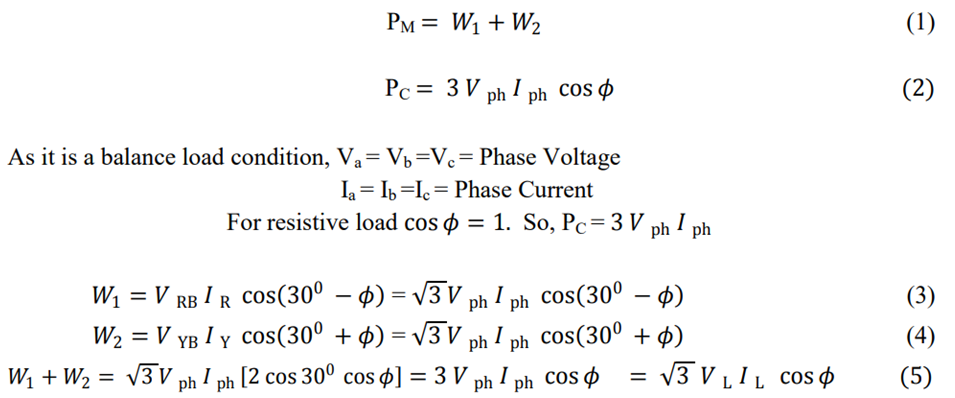Reactive Power Formula In 3 Phase
The efficient transmission and utilization of electrical power hinges on a delicate balance between real and reactive power. Recently, renewed attention has focused on understanding and accurately calculating reactive power in three-phase systems, driven by the increasing complexity of modern power grids and the integration of renewable energy sources.
At the heart of this discussion is the reactive power formula, a mathematical expression that quantifies the amount of reactive power present in a three-phase circuit. This article delves into the formula itself, its significance in power system analysis, and its implications for grid stability and energy efficiency.
Understanding Reactive Power
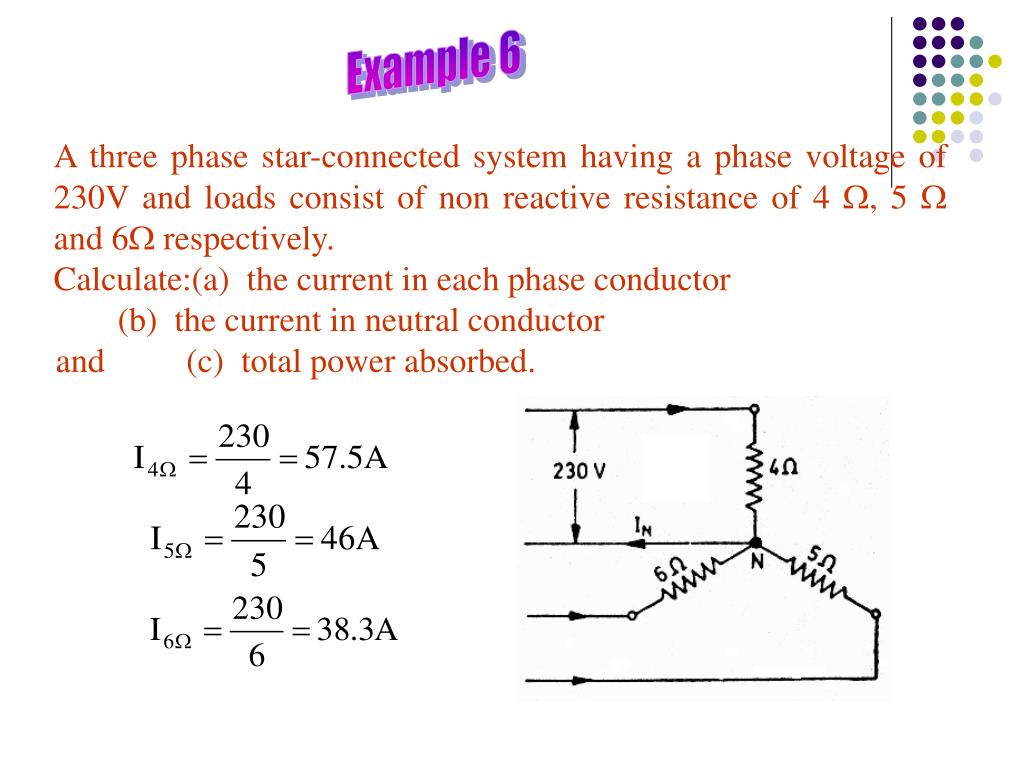
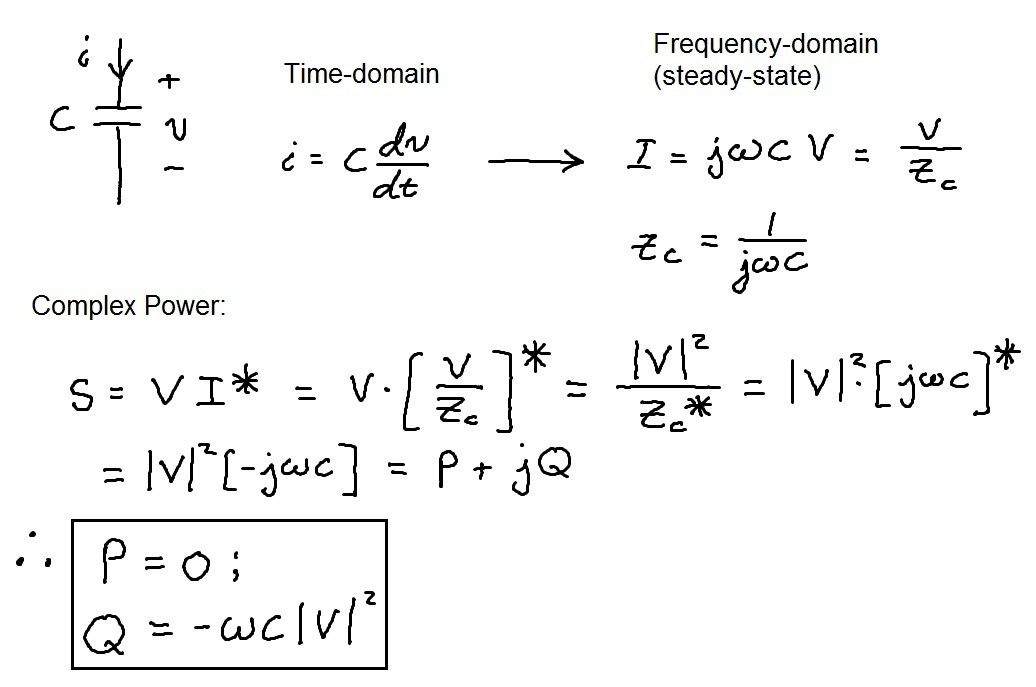
Before examining the formula, it's essential to grasp the concept of reactive power. Reactive power (Q) is the portion of electrical power that does not perform useful work but is necessary to establish and maintain electric and magnetic fields in inductive and capacitive components within a circuit.
Inductive loads, such as motors and transformers, require reactive power to create magnetic fields. Capacitive loads, like capacitors used for power factor correction, generate reactive power.
The continuous exchange of energy between the source and these reactive components results in reactive power flow, measured in volt-amperes reactive (VAR).
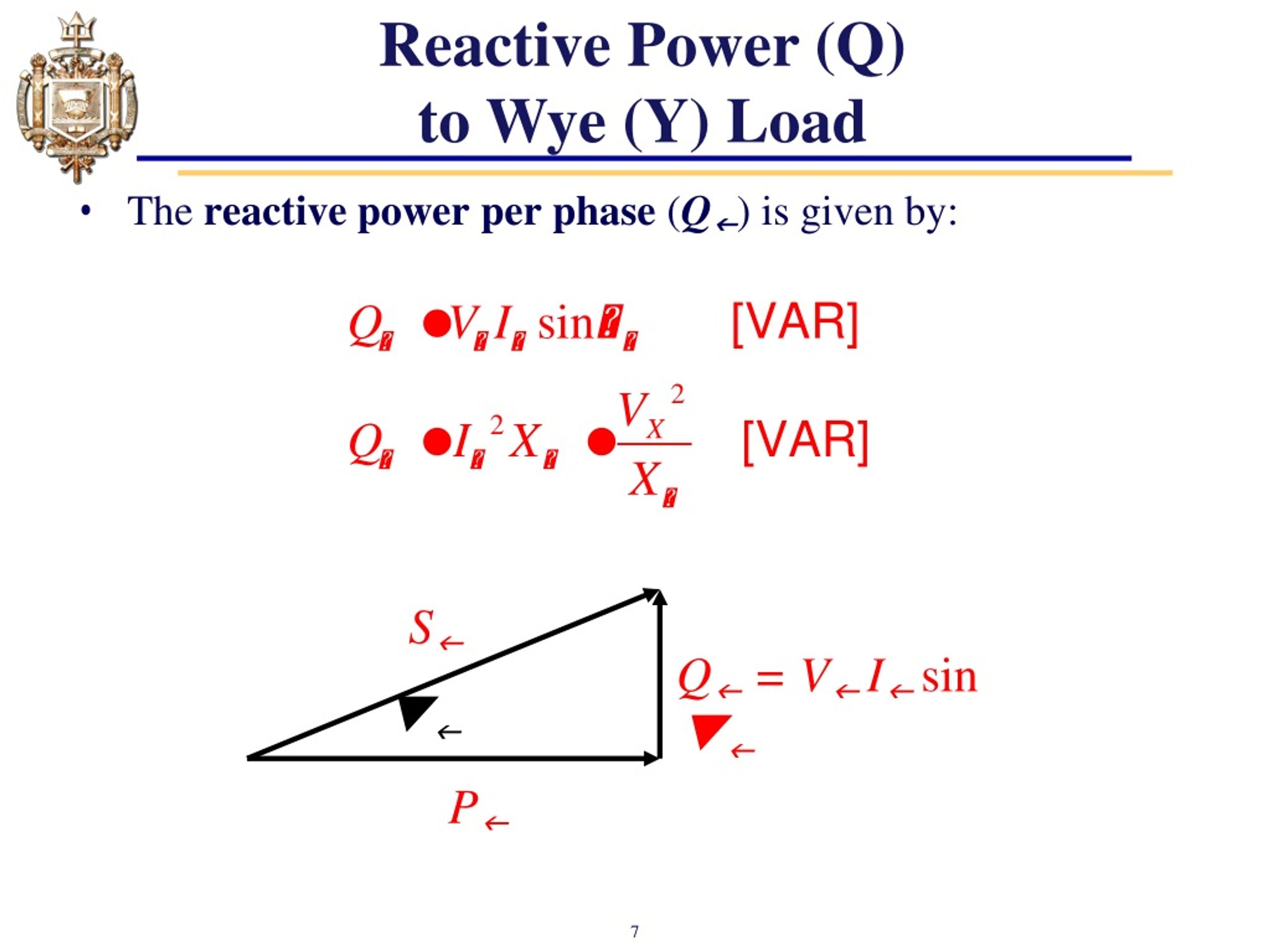
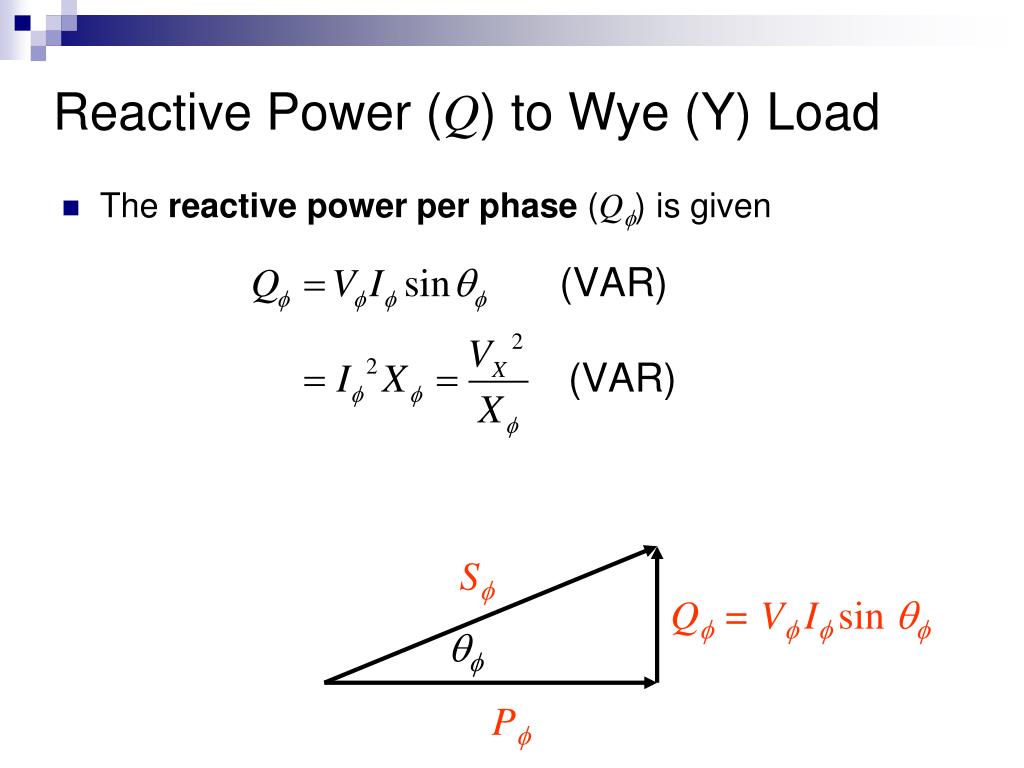
The Reactive Power Formula in Three-Phase Systems
Several formulas exist for calculating reactive power in three-phase systems, each suited to different circuit configurations and available data.
One common and widely used formula is based on line voltage and line current measurements:
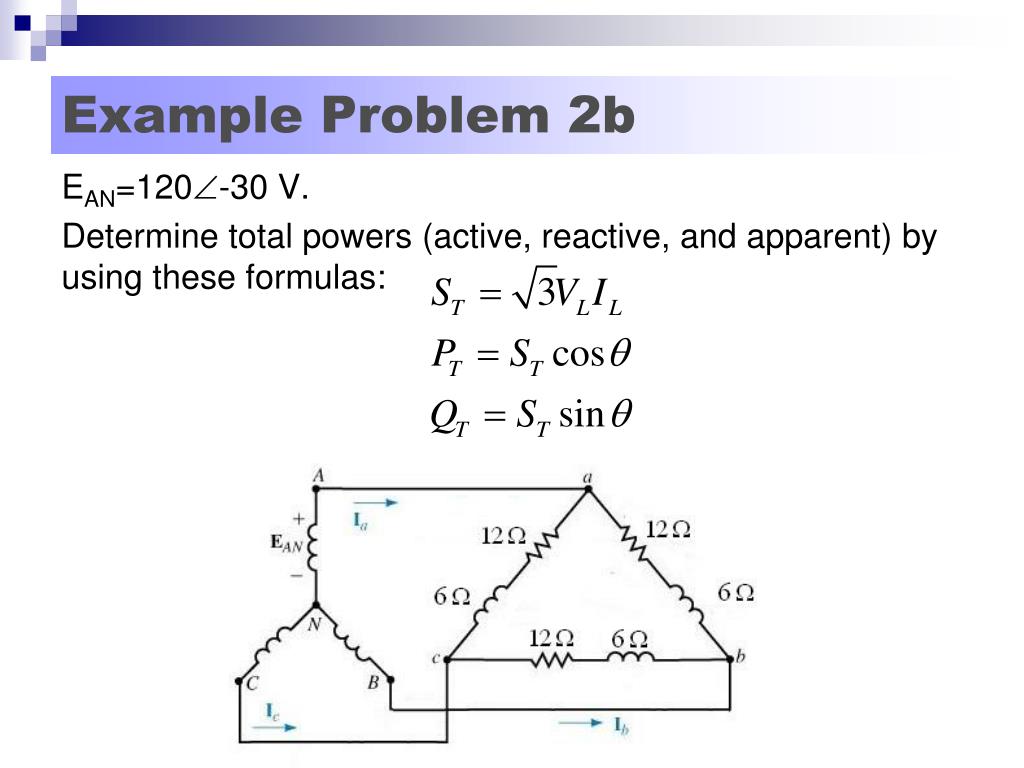
Q = √3 * VL * IL * sin(θ)
Where: VL is the line-to-line voltage, IL is the line current, and θ is the angle between the voltage and current.
Another approach uses per-phase values: Q = 3 * Vph * Iph * sin(θ), where Vph and Iph are the phase voltage and phase current, respectively.
The formula highlights the direct relationship between reactive power, voltage, current, and the power factor (cos θ). A lower power factor (closer to zero) indicates a larger phase angle and a higher proportion of reactive power.
Significance in Power System Analysis
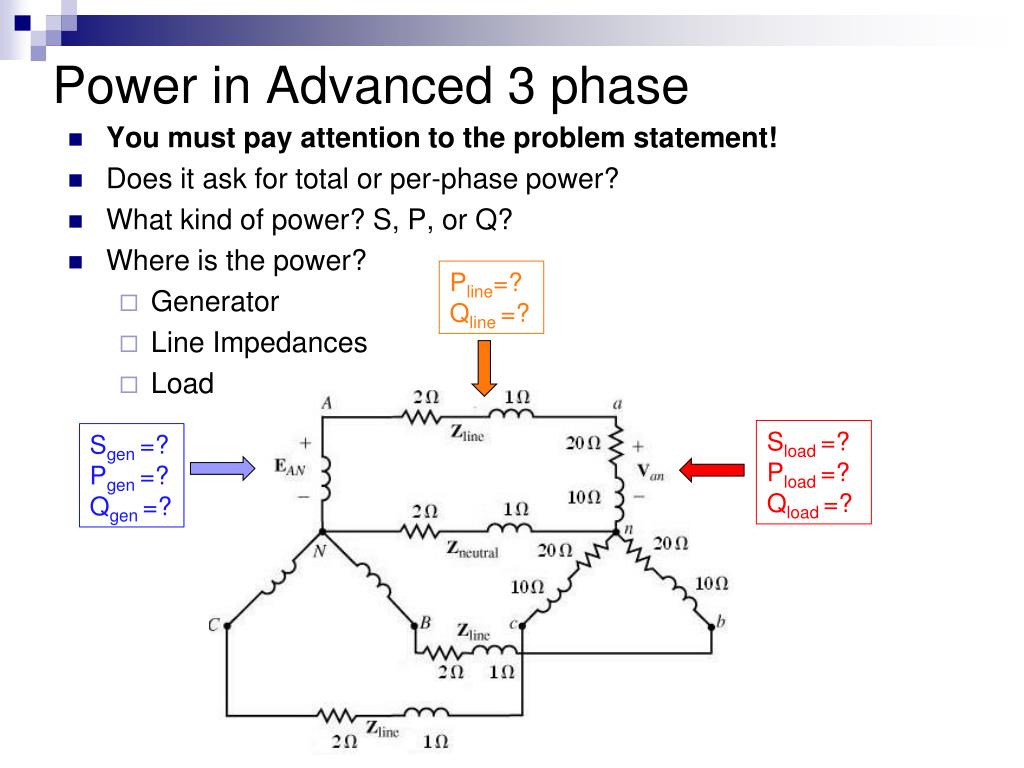
Accurate calculation of reactive power is crucial for several reasons. Power system operators rely on this information to maintain voltage stability.
Insufficient reactive power support can lead to voltage drops, potentially causing equipment malfunction or even system collapse, as stated in several reports by the North American Electric Reliability Corporation (NERC).
Managing reactive power flow helps minimize transmission losses. Excessive reactive power flow increases the current in transmission lines, leading to higher I2R losses.
Effective reactive power management is essential for maximizing the utilization of existing infrastructure and reducing the need for costly upgrades. The IEEE (Institute of Electrical and Electronics Engineers) provides detailed guidelines on reactive power control strategies.
Challenges and Future Directions
The increasing penetration of renewable energy sources, such as solar and wind, introduces new challenges in reactive power management. These sources often have intermittent output and may not inherently provide reactive power support.
Advanced technologies, such as Flexible AC Transmission Systems (FACTS) and Static VAR Compensators (SVCs), are increasingly being deployed to provide dynamic reactive power compensation. These devices can rapidly inject or absorb reactive power to maintain voltage stability and improve power quality.
Furthermore, research is ongoing to develop more sophisticated algorithms for reactive power optimization and control, leveraging advanced metering infrastructure (AMI) data and machine learning techniques.
Impact on Consumers and Society
While the intricacies of reactive power may seem abstract, its effective management has tangible benefits for consumers and society. A stable and reliable power grid ensures consistent electricity supply, minimizing disruptions and economic losses.
Efficient reactive power management also contributes to lower electricity costs. By reducing transmission losses and optimizing the use of existing infrastructure, utilities can provide electricity at a more affordable price.
Ultimately, a well-managed reactive power system is a cornerstone of a sustainable and resilient energy future, paving the way for the integration of renewable energy sources and the electrification of various sectors of the economy. The U.S. Department of Energy is actively funding research and development in this area.
Conclusion
The reactive power formula in three-phase systems is more than just a mathematical equation; it is a critical tool for understanding and managing the flow of electrical power. Its accurate application is essential for maintaining grid stability, minimizing losses, and ensuring a reliable and affordable electricity supply.
As power systems become increasingly complex, the importance of reactive power management will only continue to grow, driving innovation in technologies and strategies for optimized grid operation.



_1663164423.png)