What Are The Factors Of 96

The number 96, seemingly innocuous in its everyday appearance, unlocks a fascinating exploration into the fundamental building blocks of mathematics: its factors. Understanding these factors is not merely an academic exercise; it's a crucial skill underpinning concepts from basic arithmetic to advanced cryptography. From calculating the dimensions of a perfectly symmetrical garden bed to distributing resources equally among a group, the factors of 96 play a hidden but vital role in the world around us.

This article aims to dissect the number 96, systematically unveiling its factors and exploring the methods for identifying them. Beyond a simple listing of numbers, we will delve into the significance of prime factorization and its application in various mathematical contexts. The exploration provides a structured understanding, equipping readers with the tools to analyze and manipulate numbers more effectively.

Identifying Factors of 96: A Comprehensive Breakdown

The factors of a number are the integers that divide evenly into that number, leaving no remainder. Finding the factors of 96 involves a systematic approach, ensuring that no divisor is overlooked. Let's explore these factors methodically.

The most straightforward way to identify the factors is to start with 1 and work upwards, testing each integer to see if it divides 96 cleanly. Obviously, 1 and 96 are always factors of 96 itself. The pairs discovered through this process are the key to understanding 96's divisibility.

The Factor Pairs

We begin by identifying the factor pairs, which are two numbers that, when multiplied together, equal 96. These pairs give a clearer picture of the relationships among the factors.

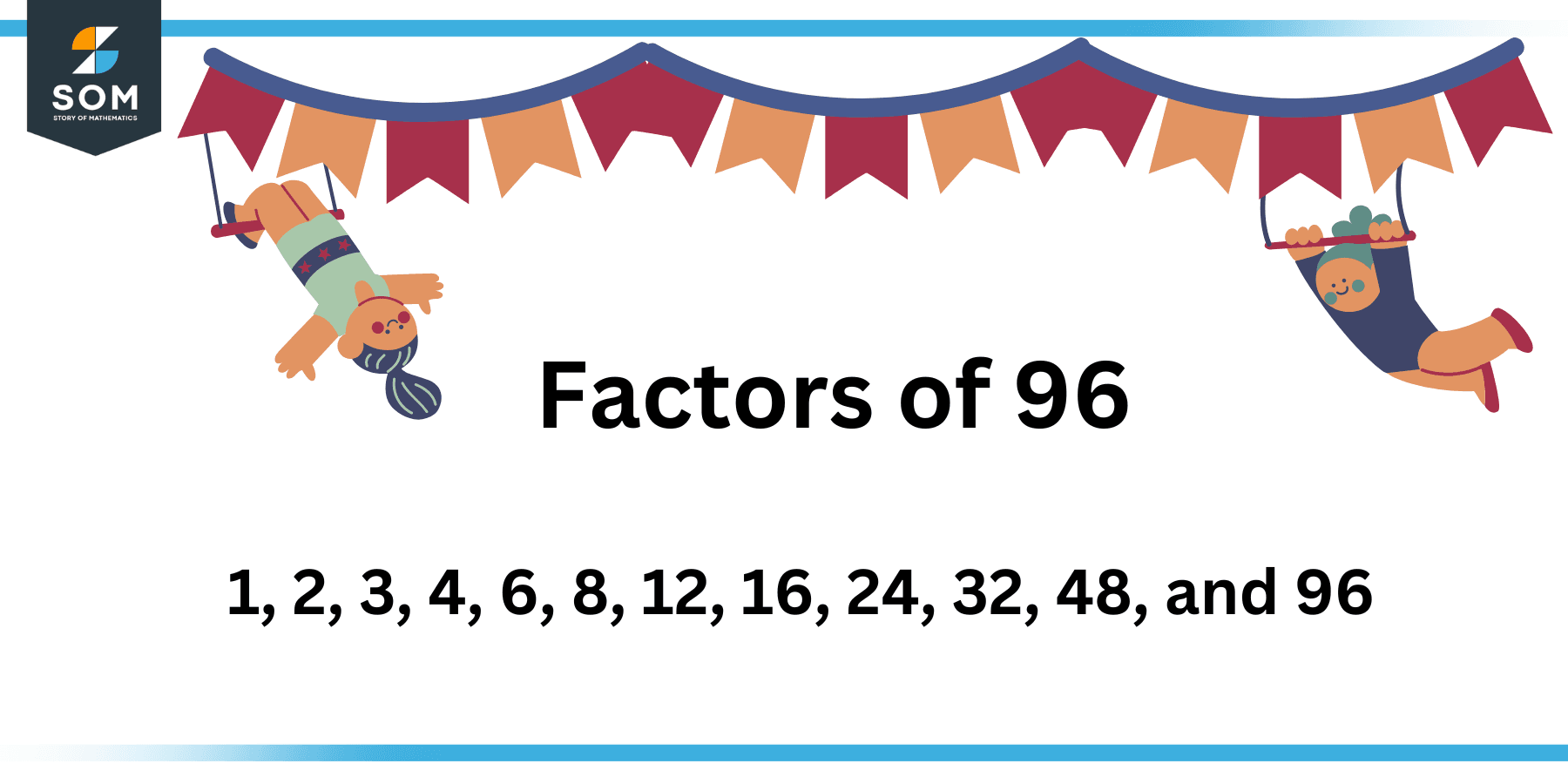
The factor pairs are: 1 x 96, 2 x 48, 3 x 32, 4 x 24, 6 x 16, and 8 x 12. Each of these pairs reveals two factors of 96. This approach reveals the comprehensive set of positive factors.

Listing All the Factors

Based on the factor pairs, we can list all the positive factors of 96 in ascending order. This ordered list offers a complete view of the divisors. It serves as a quick reference for any calculations or analyses involving 96.

Therefore, the positive factors of 96 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96. Note that all the factors are integer numbers, and divide 96 without leaving a remainder. Understanding these factors is useful in number theory and problem-solving.

Prime Factorization: Unveiling the Building Blocks

Prime factorization is the process of breaking down a number into its prime number constituents. This process provides a unique representation of any integer greater than 1. Prime factors are the smallest possible integer factors of the number.

A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Examples include 2, 3, 5, 7, and 11. These are the fundamental elements of number theory.

To find the prime factorization of 96, we can use a factor tree or division by prime numbers. Either method will lead us to the same result. Start by dividing 96 by the smallest prime number, 2.

96 ÷ 2 = 48. Then divide 48 by 2: 48 ÷ 2 = 24. Then divide 24 by 2: 24 ÷ 2 = 12.

Continue: 12 ÷ 2 = 6, and 6 ÷ 2 = 3. We end with 3 which is a prime number. We have divided 96 by 2 five times and got 3, a prime number.

Thus, the prime factorization of 96 is 2 x 2 x 2 x 2 x 2 x 3, which can be written as 2⁵ x 3. This representation is unique to 96 and demonstrates its fundamental prime constituents. Understanding prime factorization can make dealing with larger numbers much more manageable.

Applications of Factor Knowledge

Understanding the factors of numbers, including 96, has many practical applications across different fields. Here are just a few examples of where this knowledge is useful.

Resource allocation often relies on the ability to divide quantities evenly. The factors of 96 can help distribute resources such as funding or personnel across several entities. For instance, if a company has 96 employees and wants to divide them into equal-sized teams, knowing the factors of 96 would help to find the possible team sizes.

Geometry also utilizes factors when dealing with area calculations and creating shapes with specific dimensions. For example, designing a rectangular garden bed with an area of 96 square feet involves choosing dimensions that are factors of 96.

Cryptography uses prime factorization in the generation of encryption keys. While the factors of 96 are too small for practical encryption, the principles of finding factors are the underlying concepts in the encryption process.

Additionally, in computer science and data storage, knowing the factors can help optimize storage allocation and data retrieval processes. Efficiently organizing and partitioning data based on factors can improve processing speeds and reduce storage overhead.

The Significance of Factors in Number Theory

In the realm of number theory, factors are far more than mere divisors; they are the foundational building blocks of understanding integer relationships. They are deeply intertwined with concepts such as divisibility rules, greatest common divisors, and least common multiples.

The factors of a number provide valuable insights into its mathematical properties. The number of factors a number has, and the characteristics of those factors, can reveal its complexity and relationship to other numbers.

For instance, prime numbers, with their only two factors (1 and themselves), are considered the simplest building blocks. Composite numbers, like 96, have more than two factors and can be broken down into a unique prime factorization.

Moreover, the study of factors can lead to the discovery of patterns and relationships within the number system. These patterns can be exploited in various mathematical applications, from solving Diophantine equations to understanding modular arithmetic.

Looking Ahead: Continued Exploration

The journey into the factors of 96 provides a glimpse into the fascinating world of number theory. By identifying its factors and understanding its prime factorization, we gain valuable insights into the building blocks of mathematics.

Further exploration can involve examining the factors of other numbers, discovering patterns, and delving into more advanced topics such as modular arithmetic and cryptography. These are topics that students learn when taking college classes related to discrete mathematics and linear algebra.

The factors of 96 are not just numbers; they are keys to unlocking a deeper understanding of mathematics and its applications in the real world. Continued exploration of these concepts will pave the way for new discoveries and innovations across various fields.