What Is The Lcm Of 14 And 20

Imagine a rhythmic dance, two performers moving in distinct patterns. One takes steps of 14, the other of 20. When will they land on the same spot again? That moment of perfect alignment, that shared step, is mirrored in the mathematical concept of the Least Common Multiple, or LCM.
The LCM of 14 and 20 is 140. This means 140 is the smallest number that is perfectly divisible by both 14 and 20. Understanding LCM isn’t just an abstract exercise; it has practical applications in everyday life, from scheduling events to understanding gear ratios.
Unpacking the LCM: What Does It Mean?
The Least Common Multiple (LCM) is the smallest positive integer that is divisible by two or more given numbers without leaving a remainder. It's a fundamental concept in number theory with widespread use in various mathematical problems.
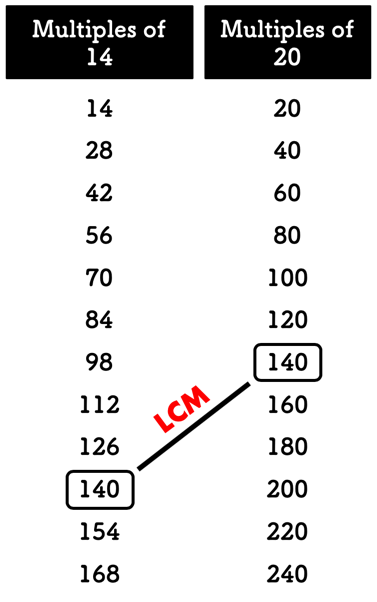
To understand the LCM, we first need to grasp the idea of multiples. Multiples are the numbers you get when you multiply a number by an integer. The multiples of 14 are 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, and so on. Similarly, the multiples of 20 are 20, 40, 60, 80, 100, 120, 140, 160, and so on.
The common multiples of 14 and 20 are the numbers that appear in both lists. In this case, some common multiples are 140, 280, and so on. The least of these common multiples is 140, hence the LCM of 14 and 20 is 140.
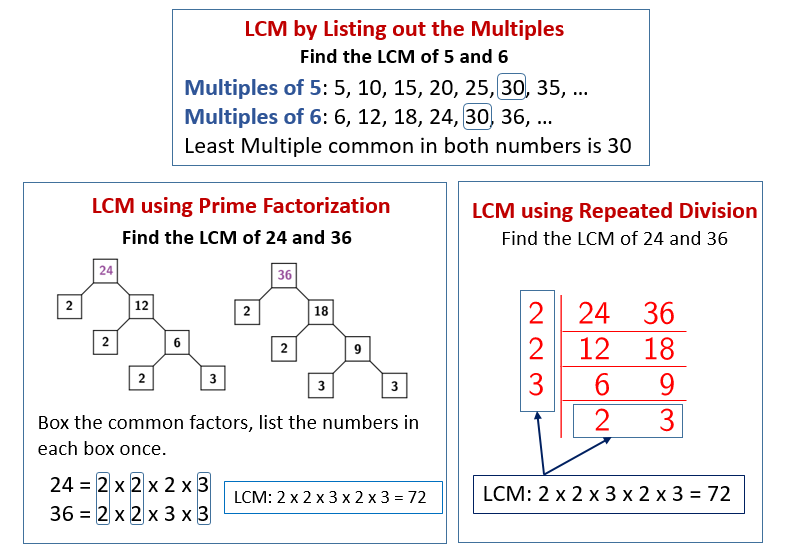
Methods for Finding the LCM
Several methods exist for finding the LCM. The most common are listing multiples, prime factorization, and using the Greatest Common Divisor (GCD).
Listing Multiples:
As demonstrated earlier, this involves listing the multiples of each number until a common multiple is found. While straightforward for small numbers, this method can become cumbersome for larger numbers.
Prime Factorization:
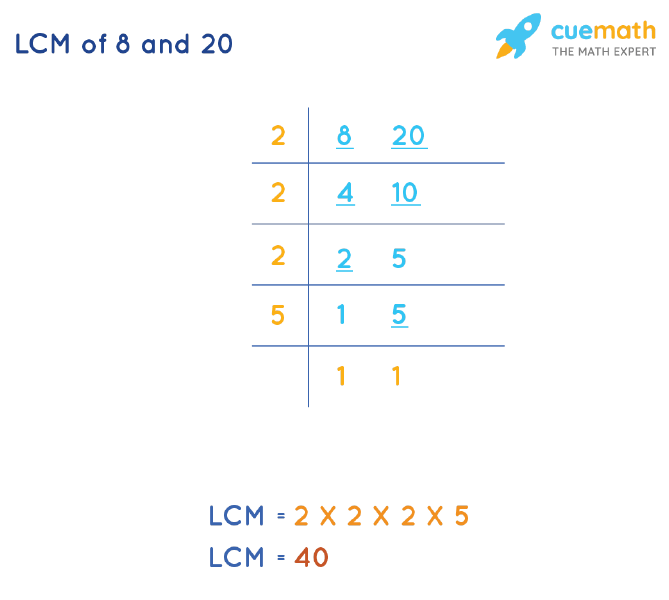
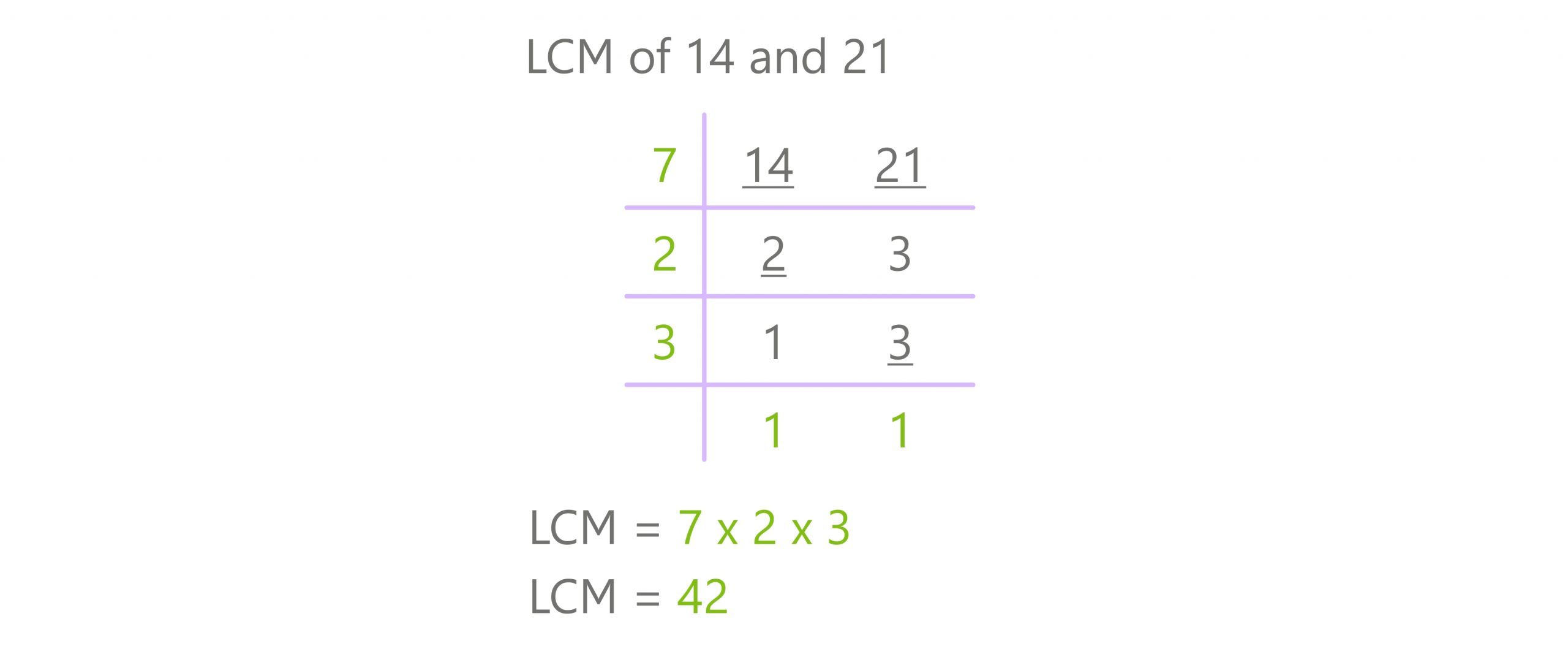
This is often the most efficient method, especially for larger numbers. It involves breaking down each number into its prime factors. First, find the prime factorization of 14 and 20.
14 = 2 x 7 and 20 = 2 x 2 x 5 or 22 x 5.
To find the LCM, take the highest power of each prime factor that appears in either factorization. So, we take 22 (from 20), 5 (from 20), and 7 (from 14). Multiply these together: 22 x 5 x 7 = 4 x 5 x 7 = 140.
Using the GCD:
The Greatest Common Divisor (GCD) is the largest number that divides two or more numbers without leaving a remainder. The relationship between the LCM and GCD is: LCM(a, b) = (a x b) / GCD(a, b).
The GCD of 14 and 20 is 2. Therefore, LCM(14, 20) = (14 x 20) / 2 = 280 / 2 = 140.
Real-World Applications of LCM
The LCM is more than just a theoretical concept. It plays a crucial role in various practical applications.
One common application is in scheduling. Imagine you have two tasks: one that needs to be done every 14 days and another that needs to be done every 20 days. The LCM (140) tells you that both tasks will need to be done on the same day every 140 days.
Another example is in cooking. When adjusting recipes for a different number of servings, the LCM can help determine the correct proportions of ingredients.
In mathematics, the LCM is used in simplifying fractions with different denominators. To add or subtract fractions, they need to have a common denominator. The LCM of the denominators serves as the least common denominator, making the calculation easier.
Furthermore, the LCM is essential in understanding gear ratios in mechanical systems. Gear ratios are expressed as fractions, and the LCM of the number of teeth on the gears helps determine the overall performance and efficiency of the system.
The Significance of Understanding LCM
Understanding the LCM strengthens your mathematical foundation. It builds upon basic arithmetic skills and introduces the concepts of multiples, factors, and prime factorization. By mastering these concepts, one can approach more complex mathematical problems with greater confidence.
The ability to find the LCM promotes problem-solving skills. It requires analytical thinking and the application of different problem-solving strategies. Students learn to analyze the problem, choose the appropriate method, and execute the solution effectively.
Beyond math class, the understanding of LCM helps with everyday life. From planning events to managing finances, the principles learned through the concept of LCM can be applied to make informed decisions.
Common Misconceptions
One common mistake is confusing the LCM with the GCD. The GCD is the greatest common divisor, while the LCM is the least common multiple. They represent opposite ends of the divisibility spectrum.
Another misconception is thinking that the LCM is always the product of the numbers. While this is true when the numbers have no common factors (other than 1), it's not generally the case. For example, 14 x 20 = 280, which is a common multiple but not the least common multiple.
Some students struggle with the prime factorization method. It's important to practice breaking down numbers into their prime factors until it becomes second nature.
Conclusion
The LCM of 14 and 20, which is 140, illustrates a beautiful blend of mathematical theory and practical application. It's a concept that connects the abstract world of numbers to the tangible world of scheduling, cooking, and engineering.
By understanding the LCM and its various methods of calculation, we empower ourselves with a valuable tool for problem-solving and critical thinking. As we continue to explore the fascinating landscape of mathematics, let us appreciate the elegance and utility of concepts like the LCM, which subtly shape our understanding of the world around us.
So, the next time you encounter a situation involving repeating cycles or proportions, remember the dance of 14 and 20, and the harmonious alignment found at 140. The LCM might just hold the key to simplifying your challenge.



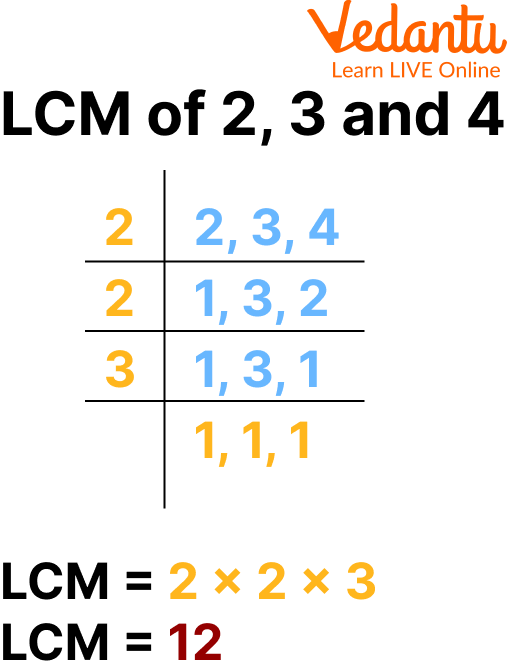





/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)