What Is The Value Of 36 Tens

In elementary mathematics, seemingly simple questions can sometimes spark deeper understanding and illuminate fundamental concepts. Recently, the question "What is the value of 36 tens?" has gained attention, serving as a powerful tool to reinforce place value and basic arithmetic skills among young learners.

At its core, determining the value of 36 tens involves multiplying 36 by 10. This exercise is not merely about arriving at the correct answer, which is 360. It's about understanding how digits shift positions when multiplied by powers of ten, and the importance of place value in the decimal system.

Understanding Place Value

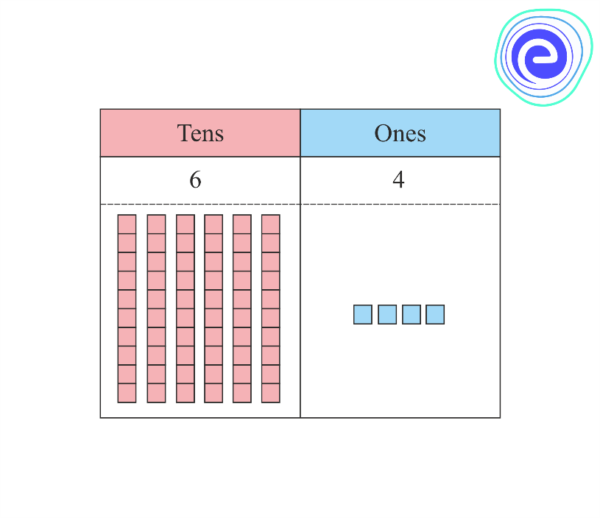
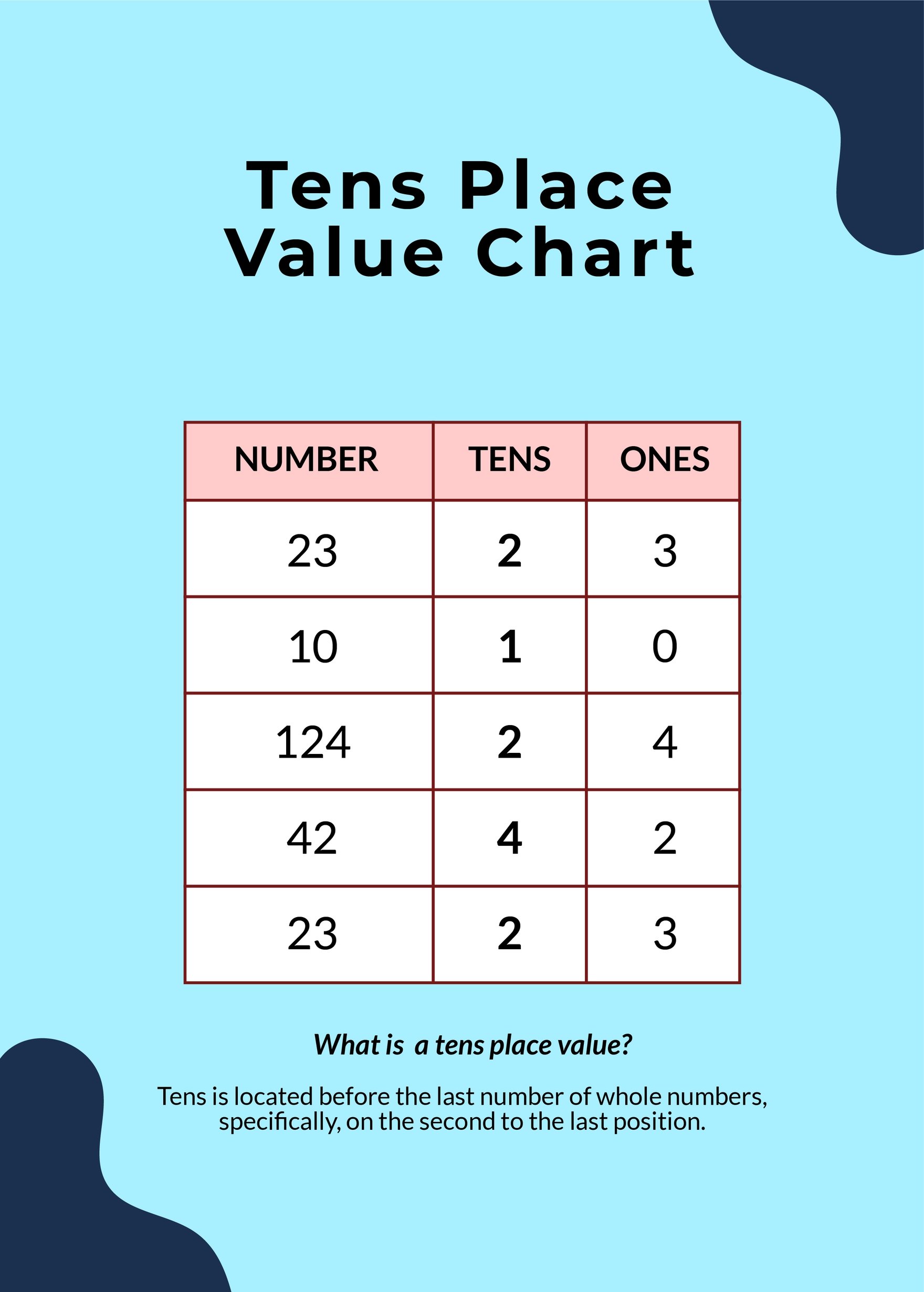
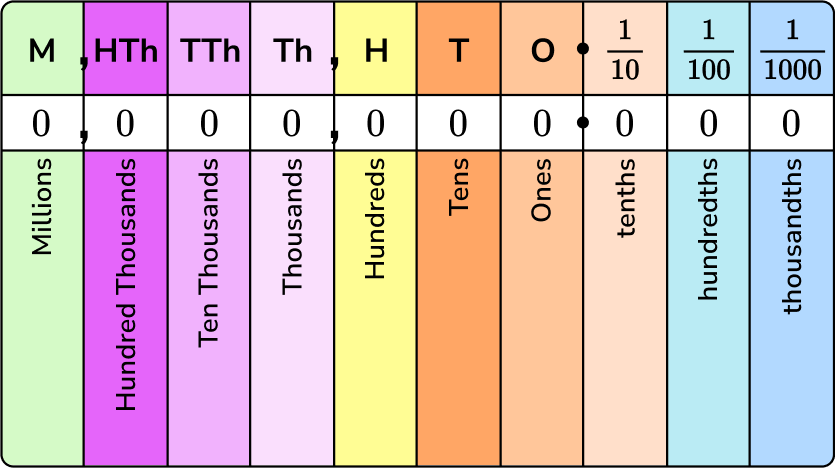
The concept of place value dictates that the position of a digit in a number determines its value. In the number 36, the '3' represents 3 tens, or 30, and the '6' represents 6 ones, or 6.

When we consider "36 tens," we're essentially asking: what number is formed when we have 36 groups of ten? This reinforces the idea that each place value represents a power of ten, and how multiplication by 10 increases the value of each digit by a factor of ten.

Calculating 36 Tens

The calculation is straightforward: 36 x 10 = 360. This result demonstrates how each digit in 36 shifts one position to the left when multiplied by 10. The '3' in the tens place (30) becomes a '3' in the hundreds place (300), and the '6' in the ones place (6) becomes a '6' in the tens place (60).

The ones place is then filled with a zero, indicating the absence of any additional ones. This concept can be further illustrated using base-ten blocks or other visual aids, allowing students to physically manipulate the numbers and observe the changes in place value.

Significance in Mathematics Education

Understanding place value is a foundational skill in mathematics education. It forms the basis for understanding larger numbers, decimals, and more complex arithmetic operations.

Questions like "What is the value of 36 tens?" offer a concrete way to solidify this understanding. By working through such problems, students develop a deeper appreciation for the structure of the number system and its inherent logic.

Experts in mathematics education emphasize the importance of not just rote memorization, but genuine conceptual understanding. "Rote memorization can lead to confusion when faced with variations of the same problem," notes Dr. Emily Carter, a professor of mathematics education at a leading university. "Conceptual understanding allows students to adapt and solve problems they may not have seen before."

Practical Applications

The ability to easily calculate multiples of ten has practical applications beyond the classroom. Estimating quantities, calculating discounts, and understanding financial concepts all rely on a firm grasp of place value and multiplication by ten.

For instance, if someone is buying 36 items that cost $10 each, quickly calculating that the total cost is $360 demonstrates the relevance of this fundamental skill.

Consider Maria Rodriguez, a small business owner. "Understanding multiples of ten helps me quickly calculate inventory costs and estimate profits," she explains. "It's a seemingly simple concept, but it's essential for day-to-day operations."

Addressing Misconceptions

Sometimes, students may struggle with the concept of place value, leading to incorrect answers. Common misconceptions include misunderstanding the role of zero as a placeholder or confusing the values of different place values.

Teachers can address these misconceptions by providing ample opportunities for hands-on practice and using visual aids to illustrate the concept. Breaking down problems into smaller, more manageable steps can also help students build confidence and solidify their understanding.

Sarah Johnson, an elementary school teacher with over 15 years of experience, advises, "Patience and repetition are key. It's crucial to address misconceptions early on and provide personalized support to struggling students."

Conclusion

The question "What is the value of 36 tens?" is more than a simple arithmetic problem. It serves as a crucial tool for reinforcing the concept of place value and developing fundamental arithmetic skills.

By mastering this concept, students build a strong foundation for future mathematical learning and develop practical skills that will benefit them throughout their lives. Continued emphasis on conceptual understanding, combined with practical applications, ensures that students not only know the answer but also understand the reasoning behind it.

As mathematics education evolves, embracing such questions as opportunities for deeper learning will undoubtedly empower students to become confident and capable problem-solvers.