What Percent Of 60 Is 15 Percent Amount And Base
The seemingly simple question of "What percent of 60 is 15?" often trips up individuals due to misunderstandings of fundamental mathematical concepts. This article delves into the nuances of percentage calculations, differentiating between the amount, base, and rate, to provide clarity and avoid common pitfalls. Understanding these core principles is crucial not only for academic purposes but also for navigating everyday financial decisions and data interpretation.
At its heart, solving percentage problems requires identifying the base (the whole), the amount (a part of the whole), and the rate (the percentage relationship between the amount and the base). Misidentifying these components leads to incorrect calculations and potentially flawed conclusions. The purpose of this investigation is to meticulously break down the question "What percent of 60 is 15?" using established mathematical principles and real-world examples, ensuring readers grasp the underlying methodology and can confidently apply it to similar scenarios.
Understanding Percentage Basics
A percentage is simply a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, understanding fractions and ratios is fundamental to mastering percentage calculations.
The three key components in percentage problems are the base, the amount, and the rate. The base is the total or the whole. The amount is the portion of the base being considered.
The rate, expressed as a percentage, represents the relationship between the amount and the base. These three elements are related by the formula: Amount = Base × Rate.
Solving "What Percent of 60 is 15?"
In the question "What percent of 60 is 15?", 60 is the base, 15 is the amount, and we are looking for the rate (the percentage). Using the formula Amount = Base × Rate, we can rearrange it to solve for the Rate: Rate = Amount / Base.
Plugging in the values, we get Rate = 15 / 60. This simplifies to Rate = 0.25. To express this as a percentage, we multiply by 100: 0.25 × 100 = 25%.
Therefore, 15 is 25% of 60. This calculation demonstrates how to accurately determine the percentage relationship between two numbers by correctly identifying the base and the amount.
Common Mistakes and How to Avoid Them
One common mistake is to incorrectly identify the base. For instance, someone might mistakenly think 15 is the base and 60 is the amount. This would lead to an incorrect calculation.
Another error involves not converting the decimal to a percentage. Dividing 15 by 60 correctly yields 0.25, but one must remember to multiply by 100 to get the percentage, 25%.
To avoid these errors, always clearly identify the whole (the base) and the part (the amount) before performing any calculations. Double-check that the final answer is expressed as a percentage.
Real-World Applications
Understanding percentage calculations is crucial in many real-world scenarios. Consider calculating discounts while shopping. A 25% discount on a $60 item is equivalent to saving $15 (25% of 60 = 15).
Percentages are also used extensively in finance. Calculating interest rates, investment returns, and loan repayments all rely on understanding percentage principles. Similarly, in business, profit margins, market share, and growth rates are often expressed as percentages.
Even in everyday life, percentages help us interpret statistics, understand survey results, and make informed decisions. For example, understanding poll data reported with percentages is crucial for informed civic engagement.
Beyond Simple Calculations: Percentage Change
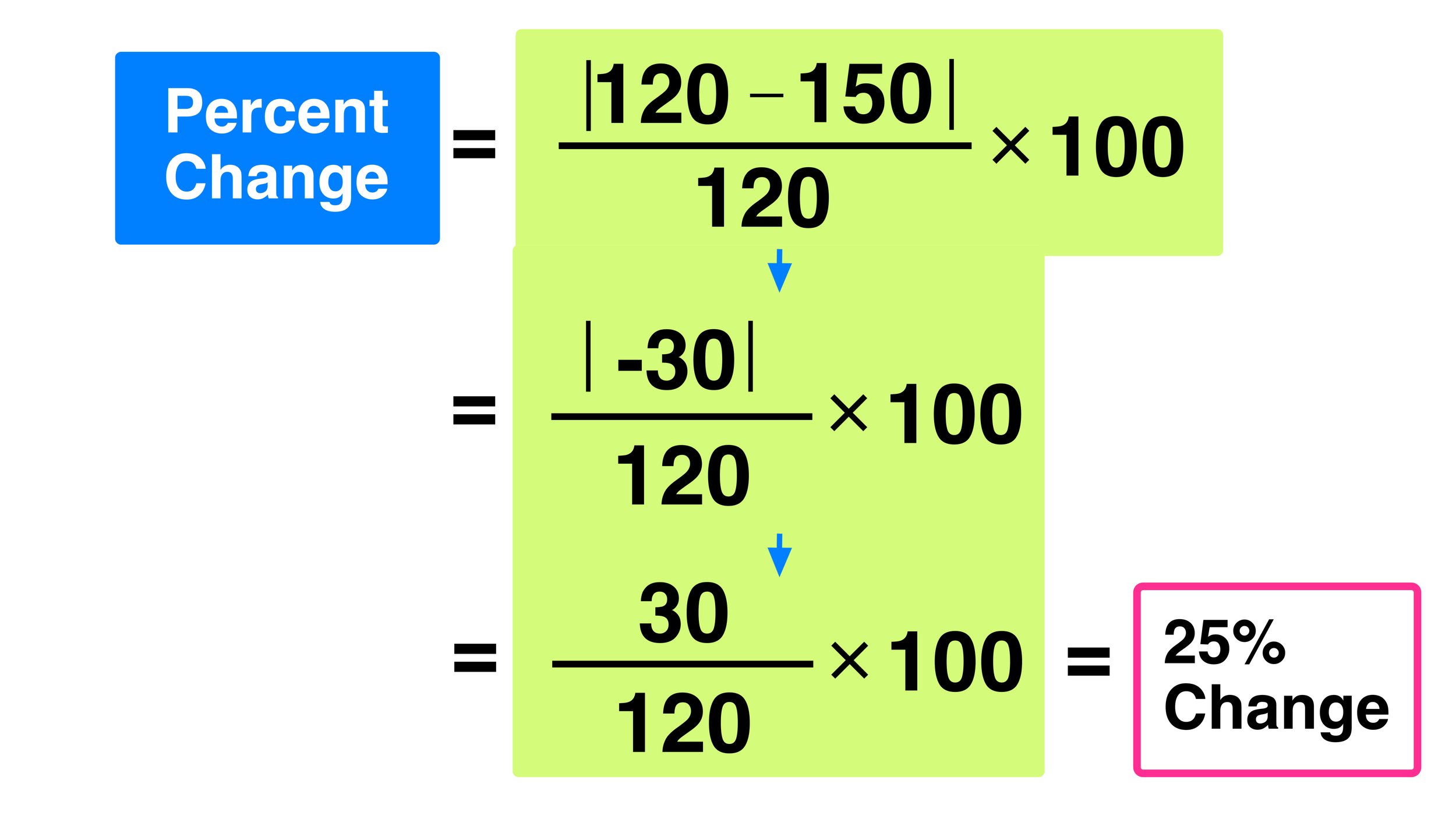
While calculating a percentage of a given number is fundamental, another important concept is percentage change. Percentage change measures the relative change between two values over time.
The formula for percentage change is: [(New Value - Old Value) / Old Value] × 100. This formula is used to calculate increases or decreases in quantities, often seen in economic data like inflation rates or stock prices.
Understanding percentage change helps in analyzing trends and making predictions based on historical data. For example, knowing that sales increased by 25% provides valuable insight into a company's performance.
The Importance of Context
Interpreting percentages correctly requires understanding the context in which they are presented. A seemingly small percentage can represent a significant absolute value depending on the base.
For example, a 1% increase in a country's GDP could represent billions of dollars. Conversely, a 99% accuracy rate on a medical test can still result in a significant number of false positives or negatives if the condition being tested is rare.
Therefore, critically evaluating the context and considering the base is essential for drawing accurate conclusions from percentage data.
Conclusion
The question "What percent of 60 is 15?" illustrates the importance of understanding the fundamental principles of percentage calculations. By correctly identifying the base, amount, and rate, individuals can accurately determine percentage relationships and avoid common errors. This knowledge is invaluable in various aspects of life, from personal finance to professional data analysis.
Moving forward, a stronger emphasis on practical application and real-world scenarios in mathematics education can further solidify students' understanding of percentages. Furthermore, continued efforts to promote data literacy will empower individuals to critically evaluate information presented using percentages, leading to more informed decision-making and a better understanding of the world around them. Ultimately, a solid grasp of percentages is not just a mathematical skill; it is a crucial tool for navigating an increasingly data-driven world.
