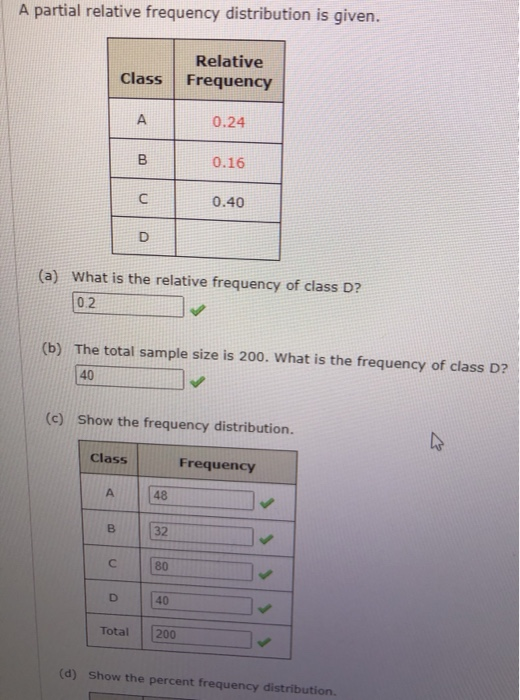
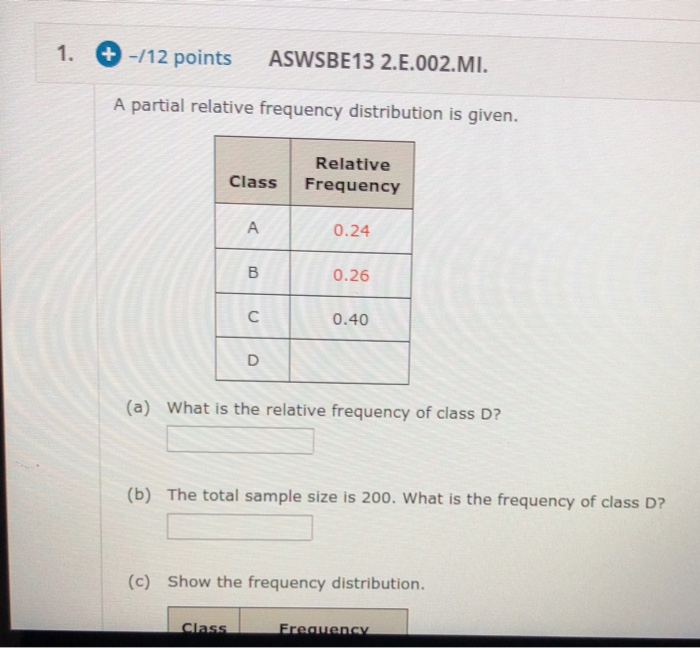
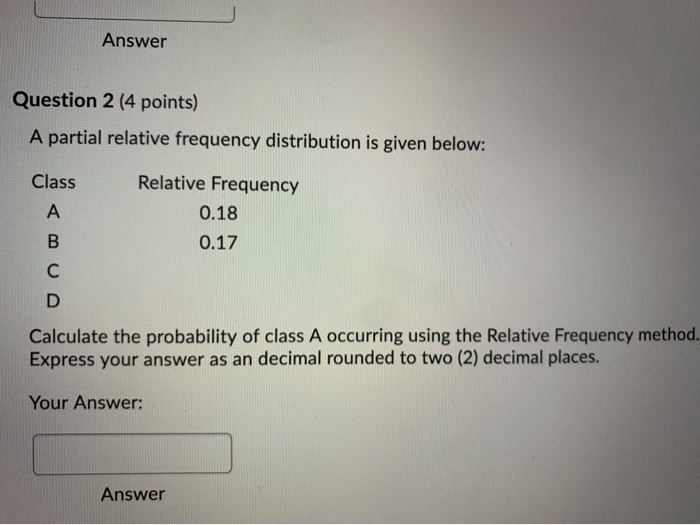
A Partial Relative Frequency Distribution Is Given

Imagine a bustling classroom, sunlight streaming through the windows, students hunched over worksheets filled with numbers and symbols. It's not a pop quiz, but rather a collaborative effort to understand a fundamental concept in statistics: the partial relative frequency distribution. This seemingly abstract idea, when unlocked, reveals powerful insights into the patterns that shape our world, from market trends to scientific discoveries.

At its core, understanding partial relative frequency distributions empowers individuals and organizations to analyze incomplete datasets, make informed decisions, and uncover hidden trends. It's a key tool in a world awash with data, enabling us to extract meaningful information from even fragmented pieces of the puzzle. The ability to interpret and work with these distributions is becoming increasingly crucial for success across diverse fields, from business to research to public policy.

Understanding Relative Frequency

Before diving into the "partial" aspect, it's essential to grasp the fundamental concept of relative frequency. Relative frequency, in its simplest form, represents the proportion of times a particular value or category appears within a dataset. It's calculated by dividing the frequency of a specific observation by the total number of observations. The result is a decimal or percentage that offers a clear picture of how common a particular value is relative to the whole.

For example, if we surveyed 100 people about their favorite color, and 30 chose blue, the relative frequency of "blue" would be 30/100, or 0.3 (30%). This immediately tells us that blue is a relatively popular choice within that sample group.

A relative frequency distribution is simply a table or graph that displays the relative frequencies for all the different values or categories in a dataset. This distribution allows for easy visual comparison of the proportions of different values. It allows patterns and trends in the data to be identified quickly.

The Challenge of Incomplete Data

In an ideal world, we'd always have complete datasets to work with, but reality often presents a different picture. Data can be lost, corrupted, or simply never collected for certain categories. This is where the concept of a partial relative frequency distribution becomes invaluable. A partial relative frequency distribution is when some of the relative frequencies are known, but some information is missing.

Consider a marketing survey where some respondents declined to answer certain questions. Or a scientific experiment where data from a few trials was lost due to equipment malfunction. In such situations, you might have a table showing relative frequencies for some categories, but with gaps representing missing data. Figuring out how to work with this is very important.

One of the main challenges is making inferences and accurate predictions using limited information. It requires careful consideration of the data you do have, the potential reasons for the missing data, and appropriate statistical techniques. It's not about guessing, but about applying sound reasoning and statistical methods to fill in the blanks.

Methods for Working with Partial Distributions

Several techniques can be employed to analyze and interpret partial relative frequency distributions. The choice of method depends on the nature of the data, the extent of the missing information, and the specific goals of the analysis.

One common approach involves estimation. Using known relative frequencies and any available information about the underlying data, you can estimate the missing values. This might involve simple proportional reasoning, more sophisticated statistical models, or domain expertise. It is important to be cautious when estimating, as estimations may not be accurate.

Another technique is hypothesis testing. Even with incomplete data, you can still test hypotheses about the distribution. By focusing on the known relative frequencies, you can assess the likelihood of certain scenarios or compare the distribution to a theoretical model.

Bayesian inference provides a framework for updating beliefs about the missing values based on the available data and prior knowledge. This approach combines the observed relative frequencies with prior probabilities to generate posterior probabilities, which reflect the updated beliefs about the unknown values.

Applications Across Industries

The ability to work with partial relative frequency distributions has wide-ranging applications across various industries. It is a valuable skillset that enhances many professions.

In market research, for example, companies often encounter incomplete survey data. By analyzing the partial relative frequencies, they can still gain insights into consumer preferences and market trends. These insights are still valuable despite some gaps.

In the field of healthcare, researchers might use partial relative frequency distributions to analyze patient data with missing records. This is useful for identifying risk factors for diseases. It also helps to evaluate the effectiveness of treatments.

Financial analysts use these techniques to assess investment risks and opportunities. This can be done by analyzing incomplete financial data. This allows them to make informed decisions despite the presence of gaps in available data.

Ethical Considerations

Working with partial relative frequency distributions also raises important ethical considerations. It is important to consider ethical implications when dealing with missing data. This is especially true when the data involves sensitive information about individuals or groups.

One key concern is the potential for bias. If the missing data is not randomly distributed, but is instead related to certain characteristics or categories, any estimations or inferences based on the partial distribution could be skewed. This could lead to unfair or discriminatory outcomes.

It is essential to be transparent about the limitations of the analysis. You must acknowledge the presence of missing data, and to carefully consider the potential biases that might arise. Researchers must also clearly communicate the assumptions and methods used to address the missing data.

Conclusion

Partial relative frequency distributions may seem like an obscure statistical concept, but they are an essential tool for navigating the complexities of real-world data. They allow you to extract meaningful insights from incomplete datasets. They offer the ability to make informed decisions even when faced with uncertainty. Mastering the techniques for working with these distributions is becoming increasingly crucial in a data-driven world.

As data continues to proliferate across every aspect of our lives, the ability to analyze and interpret fragmented information will only become more valuable. Embracing the challenge of partial relative frequency distributions is not just about mastering a statistical technique, but about developing a critical thinking mindset that can unlock hidden patterns and drive informed decision-making in an increasingly complex world.