Common Factors Of 32 And 48

In the seemingly abstract realm of mathematics, the common factors of 32 and 48 serve as a foundational concept, influencing everything from basic arithmetic to complex algorithms. Understanding these factors isn't just an academic exercise; it’s a key that unlocks a deeper understanding of numerical relationships, playing a pivotal role in everyday problem-solving and advanced technological applications.
This article delves into the common factors of 32 and 48, explaining their significance in various contexts. We will explore how these seemingly simple numbers can impact fields ranging from computer science to financial analysis, highlighting their importance in the grand scheme of mathematical understanding. It aims to present a clear, concise overview of this topic, illustrating its practical applications and theoretical underpinnings.
Understanding Factors and Common Factors
A factor of a number is an integer that divides the number evenly, leaving no remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. Common factors, then, are the factors that two or more numbers share.
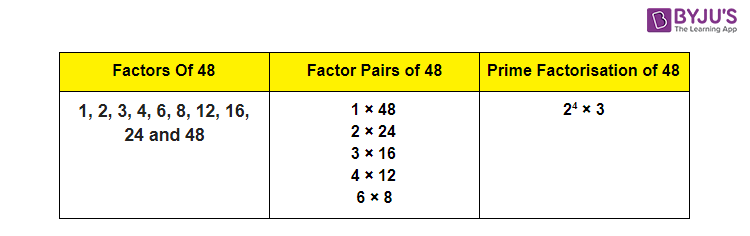
To find the common factors of 32 and 48, we must first identify all the factors of each number individually. The factors of 32 are 1, 2, 4, 8, 16, and 32. The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
Comparing these lists, we can see that the common factors of 32 and 48 are 1, 2, 4, 8, and 16. The largest of these, 16, is known as the Greatest Common Factor (GCF), sometimes called the Highest Common Factor (HCF).
The Greatest Common Factor (GCF)
The GCF, or HCF, is the largest number that divides evenly into two or more numbers. In the case of 32 and 48, the GCF is 16. This means that 16 is the largest number by which both 32 and 48 can be divided without leaving a remainder.
The GCF has numerous applications, particularly in simplifying fractions. For example, the fraction 32/48 can be simplified by dividing both the numerator and the denominator by their GCF, 16, resulting in the simplified fraction 2/3.
Beyond fraction simplification, the GCF is vital in algebra and number theory, serving as a basis for many mathematical proofs and operations. It's a foundational concept that bridges basic arithmetic and more complex mathematical concepts.
Methods for Finding Common Factors
There are several methods for finding the common factors of two numbers. The most straightforward method is listing all the factors of each number, as demonstrated earlier.
Another method involves prime factorization. Prime factorization is the process of breaking down a number into its prime factors. For example, the prime factorization of 32 is 2 x 2 x 2 x 2 x 2 (or 25), and the prime factorization of 48 is 2 x 2 x 2 x 2 x 3 (or 24 x 3).
To find the GCF using prime factorization, identify the common prime factors and their lowest powers. In this case, both numbers share the prime factor 2, and the lowest power of 2 present in both factorizations is 24, which equals 16. Thus, the GCF is 16.
Real-World Applications
Understanding common factors extends beyond the classroom and has practical applications in various fields. In computer science, the GCF is used in cryptography and data compression algorithms.
For instance, the GCF can help optimize data storage by identifying redundant patterns. According to Dr. Anya Sharma, a computer science professor at MIT, “Efficient algorithms that rely on concepts like the GCF are critical for handling the vast amounts of data generated daily.”
In architecture and design, common factors are used to divide spaces equally or create symmetrical designs. Construction projects rely on the GCF to ensure that materials are used efficiently and that measurements are precise.
Implications for Education
Teaching the concept of common factors effectively is crucial for building a strong foundation in mathematics. Many educators are focusing on interactive and hands-on approaches to engage students.
Professor David Lee, a mathematics educator at Stanford University, emphasizes the importance of relating mathematical concepts to real-world scenarios. "When students understand the practical relevance of concepts like common factors, they are more likely to grasp and retain the information," he notes.
Curriculum developers are increasingly incorporating problem-solving activities that require students to apply their knowledge of common factors in different contexts. This approach aims to foster critical thinking skills and enhance students' overall mathematical proficiency.
Looking Ahead
The concept of common factors remains relevant in both theoretical and applied mathematics. As technology advances, the applications of these fundamental principles will continue to evolve.
Future research might explore the use of common factors in more complex algorithms and cryptographic systems. Continuous innovation in these areas depends on a solid understanding of foundational mathematical concepts.
Ultimately, the common factors of 32 and 48, while seemingly simple, represent a gateway to a deeper understanding of mathematics and its impact on the world around us. Their importance in various fields highlights the interconnectedness of mathematical theory and practical applications.