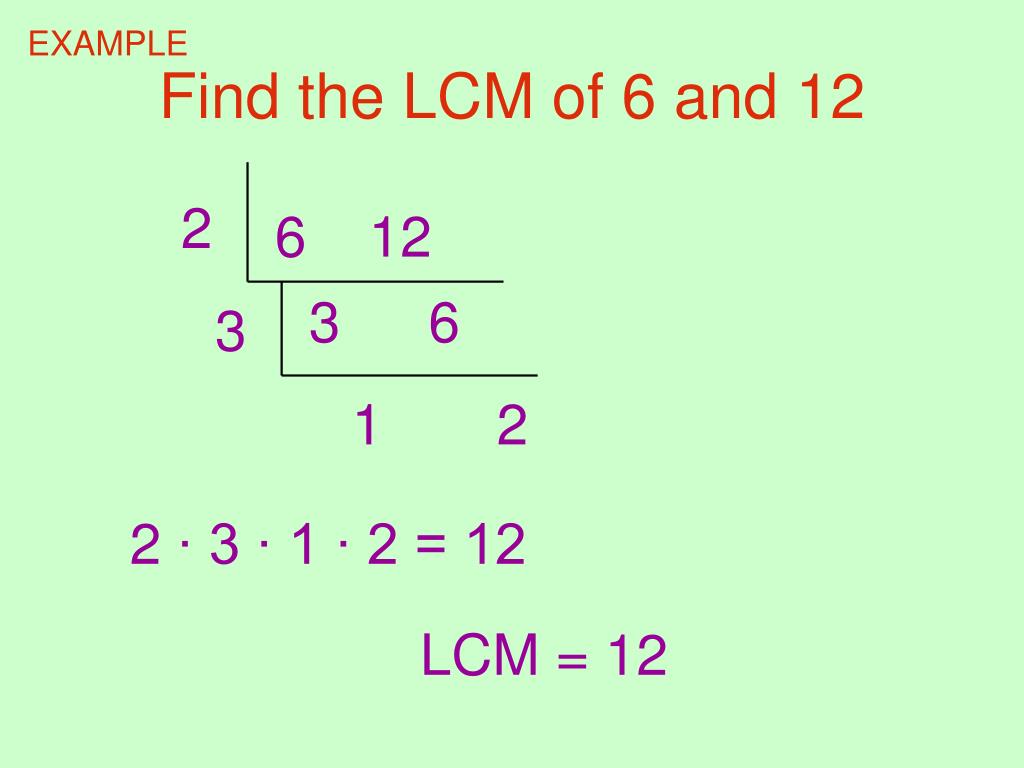
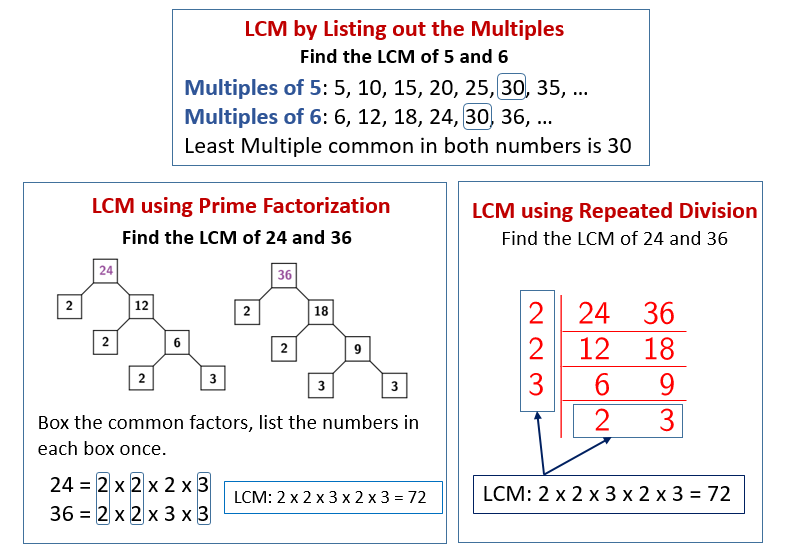
What Is The Lcm Of 8 12 And 15

In classrooms and beyond, the pursuit of mathematical clarity often hinges on seemingly simple questions. One such question, "What is the Least Common Multiple (LCM) of 8, 12, and 15?" unlocks a fundamental concept applicable to diverse fields, from scheduling tasks to understanding musical harmony. The answer, however, requires a methodical approach, highlighting the importance of prime factorization and careful calculation.

The LCM, or Least Common Multiple, is the smallest positive integer that is perfectly divisible by each of the given numbers. For 8, 12, and 15, finding this value is crucial in problem-solving across various domains. This article delves into the methods for determining the LCM, exploring its practical applications and its significance in mathematical understanding. Understanding LCM can simplify fractions, design efficient schedules, and reveal patterns in numerical relationships.

Understanding the Least Common Multiple

The LCM, a cornerstone of number theory, plays a vital role in simplifying mathematical operations involving fractions. It represents the smallest multiple shared by a set of numbers. This value is key when adding or subtracting fractions with different denominators, as it provides the common ground needed to perform these operations seamlessly.

Consider the fractions 1/8, 1/12, and 1/15. To add these, you need a common denominator. The LCM of 8, 12, and 15 provides this common denominator, allowing for easier calculation.

Methods for Finding the LCM

There are several methods for finding the LCM, each with its advantages and suitability for different sets of numbers. Two prominent approaches are the listing method and the prime factorization method. Understanding both provides a versatile toolkit for tackling LCM problems.

The listing method involves listing multiples of each number until a common multiple is found. While straightforward for small numbers, this method can become cumbersome for larger numbers.

The prime factorization method, on the other hand, breaks down each number into its prime factors. It is considered a more efficient and systematic approach, especially for larger numbers.

Prime Factorization: A Detailed Approach

Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. For example, 2, 3, 5, 7, and 11 are prime numbers.

Let's apply prime factorization to 8, 12, and 15. First, we find the prime factors of each number: 8 = 2 x 2 x 2 = 2³, 12 = 2 x 2 x 3 = 2² x 3, and 15 = 3 x 5.

To find the LCM, we take the highest power of each prime factor that appears in any of the factorizations. Here, the prime factors are 2, 3, and 5. The highest power of 2 is 2³, the highest power of 3 is 3¹, and the highest power of 5 is 5¹.

Therefore, the LCM of 8, 12, and 15 is 2³ x 3 x 5 = 8 x 3 x 5 = 120. This means 120 is the smallest number divisible by 8, 12, and 15.

Practical Applications of LCM

The LCM isn't just an abstract mathematical concept; it has real-world applications. These applications span diverse fields, demonstrating its practical utility.

In scheduling, the LCM can be used to determine when events will coincide. Imagine three buses that leave a station at different intervals: every 8 minutes, 12 minutes, and 15 minutes respectively. The LCM, 120, indicates that all three buses will leave the station together every 120 minutes.

In music, the LCM helps understand rhythmic patterns and harmonies. Different musical notes have frequencies that can be related through mathematical ratios, and the LCM can help determine the duration of a musical phrase or cycle.

"Understanding the LCM is not just about finding a number; it's about grasping a concept that unlocks solutions to real-world problems." - Dr. Anya Sharma, Professor of Mathematics

Common Mistakes and How to Avoid Them

While the process of finding the LCM is relatively straightforward, some common mistakes can lead to incorrect results. One frequent error is misidentifying prime numbers.

Another mistake is overlooking factors during prime factorization, resulting in an incomplete factorization. Careful checking is essential at each step of the process.

A further error can occur when calculating the LCM from the prime factors. Forgetting to take the highest power of each prime factor will give an incorrect result.

Conclusion

The LCM of 8, 12, and 15 is 120. This seemingly simple calculation reveals a powerful mathematical concept with widespread applications.

By understanding the methods for finding the LCM and its practical applications, individuals can enhance their problem-solving skills in mathematics and various fields. As we've seen, the ability to find the LCM facilitates tasks ranging from simplifying fractions to designing efficient schedules. The value of the LCM extends far beyond the classroom, underscoring its fundamental importance in quantitative reasoning and real-world applications.